甲、乙两地之间有一条笔直的公路L，小明从甲地出发沿公路ι步行前往乙地，同时小亮从乙地出发沿公路L骑自行车前往甲地，小亮到达甲地停留一段时间，原路原速返回，追上小明后两人一起步行到乙地．设小明与甲地的距离为y1米，小亮与甲地的距离为y2米，小明与小亮之间的距离为s米，小明行走的时间为x分钟．y1、y2与x之间的函数图象如图1，s与x之间的函数图象（部分）如图2．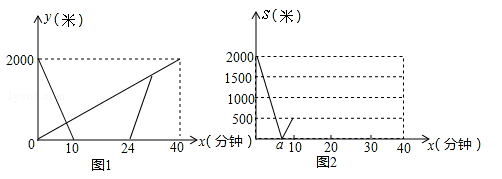
（1）求小亮从乙地到甲地过程中y1（米）与x（分钟）之间的函数关系式；
（2）求小亮从甲地返回到与小明相遇的过程中s（米）与x（分钟）之间的函数关系式；
（3）在图2中，补全整个过程中s（米）与x（分钟）之间的函数图象，并确定a的值．
如图，在平面直角坐标系中，点 A（5,0），B（3,2），点C在线段OA上，BC=BA，点Q是线段BC上一个动点，点P的坐标是（0,3），直线PQ的解析式为y=kx+b（k≠0），且与x轴交于点D．
（1）求点C的坐标及b的值；
（2）求k的取值范围；
（3）当k为取值范围内的最大整数时，过点B作BE∥x轴，交PQ于点E，若抛物线y=ax2﹣5ax（a≠0）的顶点在四边形ABED的内部，求a的取值范围．
如图1，在□ABCD中，点E是BC边上的中点，点F是线段AE上一点，BF的延长线交射线CD于点G，若AB=6，
，求DG的长．
小米的发现，过点E作
交BG于点H（如图2），经过推理和计算能够使问题得到解决．则DG=．
如图3，四边形ABCD中，AD∥BC，点E是射线DM上的一点，连接BE和AC相交于点F，若
，
，求
的值（用含
的代数式表示）．
如图，已知，⊙O为△ABC的外接圆，BC为直径，点E在AB边上，过点E作EF⊥BC，延长FE交⊙O的切线AG于点G．
（1）求证：GA=GE．
（2）若AC=6，AB=8，BE=3，求线段OE的长．
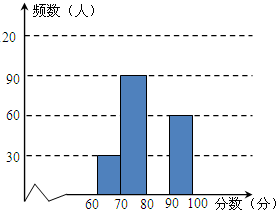
2015年是中国抗日战争胜利70周年暨世界反法西斯战争胜利70周年．某校为纪念中国抗日战争胜利70周年，对全校学生进行了“抗日战争知多少”知识测验．然后随机抽取了部分学生的成绩，整理并制作如图所示的图表．
请你根据图表中提供的信息，解答下列问题：
| 分数段 |
频数 |
频率 |
| 60≤x＜70 |
30 |
0．1 |
| 70≤x＜80 |
90 |
m |
| 80≤x＜90 |
n |
0．4 |
| 90≤x＜100 |
60 |
0．2 |
（1）在频数分布表中：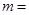
________，
________；
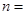（2）补全频数分布直方图；
（3）如果某校有2000名学生，比赛成绩80分以上（含80分）为优秀，那么你估计此次测验成绩的优秀人数大约是__________人．
列方程或方程组解应用题：
为开阔学生的视野在社会大课堂活动中，某校组织初三年级学生参观科技馆，原计划租用45座客车若干辆，但有15人没有座位；若租用同样数量的60座客车，则多出一辆车，且其余客车恰好坐满．求该校初三年级有学生多少人？原计划租用多少辆45座客车？