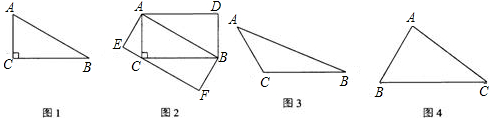
阅读下面短文：如图1，△ABC是直角三角形，∠C=90°，现将△ABC补成长方形，使△ABC的两个顶点为长方形一边的两个端点，第三个顶点落在长方形这一边的对边上，那么符合要求的长方形可以画出两个：长方形ACBD和长方形AEFB（如图2）。
解答问题：
（1）设图2中长方形ACBD和长方形AEFB的面积分别为S1，S2，则S1 S2（填“＞”、“＝”或“＜”）
（2）如图3，△ABC是钝角三角形，按短文中的要求把它补成长方形，那么符合要求的长方形可以画出 个，利用图3把它画出来。
（3）如图4，△ABC是锐角三角形且三边满足BC＞AC＞AB，按短文中的要求把它补成长方形，那么符合要求的长方形可以画出 个，利用图4把它画出来。
（4）在（3）中所画出的长方形中，哪一个的周长最小？为什么？
某城市一年中最低气温为﹣2℃，若用t（单位：℃）表示该城市气温，则如何表示该城市气温的变化情况？
已知方程组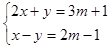
，试列出使x＞y成立的关于m的不等式．
某市自来水公司按如下标准收取水费：若每户每月用水不超过10m3，则每立方米收费1.5元；若每户每月用水超过10m3，则超过的部分每立方米收费2元．小亮家某月的水费不少于25元，那么他家这个月的用水量（xm3）至少是多少？请列出关于x的不等式．
某学校为学生安排宿舍，现有住房若干间，若每间5人，则还有14人安排不下，若每间7人，则有一间不足7人．问学校至少有几间房可以安排学生住宿？可以安排住宿的学生有多少人？
（1）列式：x与20的差不小于0；
（2）若（1）中的x（单位：cm）是一个正方形的边长，现将正方形的边长增加2cm，则正方形的面积至少增加多少？