菱形ABCD中，∠ABC=450，点P是对角线BD上的任一点，点P关于直线AB、AD、CD、BC的对称点分别是点E、F、G、H， BE与DF相交于点M，DG与BH相交于点N，证明:四边形BMDN是正方形。
如图所示，将长方形ABCD沿直线BD折叠，使C点落在C′处，BC′交AD于E．
（1）求证：BE=DE；
（2）若AD=8，AB=4，求△BED的面积．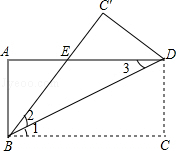
已知：y=y1+y2，y1与x2成正比例，y2与x成反比例，且x=1时，y=3；x=﹣1时，y=1．求x=﹣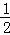
时，y的值．
问题探索
（1）计算与观察：把
的分子分母同时加上1，得到
，把
的分子分母同时加上2，得到
．比较
的大小关系： 
， （填“＞”、“＜”）
（2）归纳猜想：若正分数
（a＞b＞0）中的分子和分母同时加上正数m，得到
，结论又如何呢？ （填“＞”、“＜”）
（3）请证明你的猜想：
（1）已知在△ABC中，AB=
，AC=
，BC=5，则△ABC的形状为 ．（直接写出结果）
（2）试在4×4的方格纸上画出△ABC，使它的顶点都在方格的顶点上．（每个小方格的边长为1）
（1）计算：
（2）解方程：
．