阅读下列材料:
小华遇到这样一个问题,如图1,△ABC中,∠ACB=30º,BC=6,AC=5,在△ABC内部有一点P,连接PA.PB.PC,求PA+PB+PC的最小值.
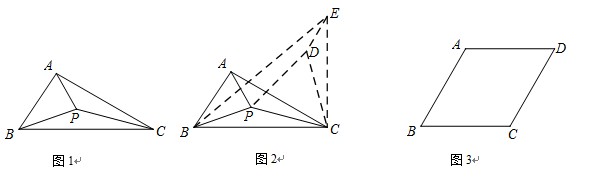
小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折.旋转.平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC绕点C顺时针旋转60º,得到△EDC,连接PD.BE,则BE的长即为所求.
(1)请你写出图2中,PA+PB+PC的最小值为 ;
(2)参考小华的思考问题的方法,解决下列问题:
①如图3,菱形ABCD中,∠ABC=60º,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段(保留画图痕迹,画出一条即可);
②若①中菱形ABCD的边长为4,请直接写出当PA+PB+PC值最小时PB的长.
(本题12分)阅读下列材料并解决有关问题:
我们知道 现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式
现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式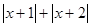 时,可令
时,可令 和
和 ,分别求得
,分别求得 和
和 (称
(称 ,
, 分别为
分别为 与
与 的零点值).在有理数范围内,零点值
的零点值).在有理数范围内,零点值 和
和 可将全体有理
可将全体有理数分成不重复且不遗漏的如下 种情况:(1)
种情况:(1) ;(2)
;(2) ;(3)
;(3) .从而化简代数式
.从而化简代数式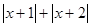 可分以下
可分以下 种情况:
种情况:
(1)当 时,原式
时,原式 ;
;
(2)当 时,原式
时,原式 ;
;
(3)当 时,原式
时,原式 .
.
综上讨论,原式
通过以上阅读,请你解决以下问题:
(1)分别求出 和
和 的零点值;
的零点值;
(2)化简代数式 ;
;
(3)解方程 .
.
(本题10分)用正方形硬纸板做三棱柱盒子,每个盒子由 个矩形侧面和
个矩形侧面和 个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用) 方法:剪
方法:剪 个侧面;
个侧面; 方法:剪
方法:剪 个侧面和
个侧面和 个底面.
个底面.
现有 张硬纸板,裁剪时
张硬纸板,裁剪时 张用
张用 方法,其余用
方法,其余用 方法.
方法.
(1)用 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
(本题10分)已知关于 的方程
的方程 和
和 有相同的解,求
有相同的解,求 的值和这个解是什么?
的值和这个解是什么?
(本题10分)小强在计算一个整式减去 时,因为粗心,把减去误作为加上,得结果为
时,因为粗心,把减去误作为加上,得结果为 .试问:
.试问:
(1)这是一个怎样的整式?
(2)原题的正确结果应是多少?
(本题10分)某出租车一天下午以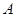 地为出发地在东西方向运营,向东走为正,向西走为负,行车里程(单位:
地为出发地在东西方向运营,向东走为正,向西走为负,行车里程(单位: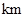 )依先后顺序记录如下:
)依先后顺序记录如下: ,
,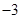 ,
, ,
, ,
, ,
,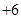 ,
,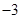 ,
, ,
,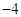 ,
, .将最后一名乘客送到目的地,出租车离
.将最后一名乘客送到目的地,出租车离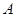 地多远?在
地多远?在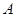 地的什么方向?若每千米的价格为
地的什么方向?若每千米的价格为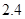 元,司机一个下午的营业额是多少?
元,司机一个下午的营业额是多少?