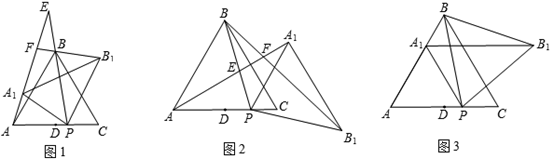
如图1，在等边△ABC中，点D是边AC的中点，点P是线段DC上的动点(点P与点C不重合)，连结BP. 将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P,连结AA1，射线AA1分别交射线PB、射线B1B于点E、F.
（1）如图1，当0°＜α＜60°时，在α角变化过程中，△BEF与△AEP始终存在 关系（填“相似”或“全等”），并说明理由；
（2）如图2，设∠ABP="β" . 当60°＜α＜180°时，在α角变化过程中，是否存在△BEF与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由；
（3）如图3，当α=60°时，点E、F与点B重合. 已知AB=4，设DP=x，△A1BB1的面
积为S，求S关于x的函数关系式.
直线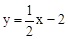
与x、y轴分别交于点A、C．抛物线的图象经过A、C和点B（1，0）．
（1）求抛物线的解析式；
（2）在直线AC上方的抛物线上有一动点D，当D与直线AC的距离DE最大时，求出点D的坐标，并求出最大距离是多少？
已知：⊙O的直径为3，线段AC=4，直线AC和PM分别与⊙O相切于点A，M．
（1）求证：点P是线段AC的中点；
（2）求sin∠PMC的值．
某校为了丰富学生的校园生活，准备购进一批篮球和足球．其中篮球的单价比足球的单价多40元，用1500元购进的篮球个数与900元购进的足球个数相等．
（1）篮球和足球的单价各是多少元？
（2）该校打算用1000元购买篮球和足球，问恰好用完1000元，并且篮球、足球都买有的购买方案有哪几种？
如图，D是△ABC的边AB上一点，CN∥AB，DN交AC于点M，若MA=MC．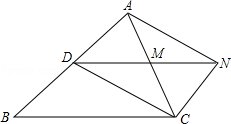
（1）求证：CD=AN；
（2）若AC⊥DN，∠CAN=30°，MN=1，求四边形ADCN的面积．
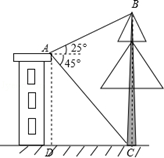
如图，小明在楼上点A处测量大树的高，在A处测得大树顶部B的仰角为25°，测得大树底部C的俯角为45°．已知点A距地面的高度AD为12m，求大树的高度BC．（最后结果精确到0.1）