如图,已知菱形ABCD的边长为4,∠A=60°,对称中心为点P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=60°,图中两块阴影部分图形关于直线AC成轴对称,设它们的面积和为S1.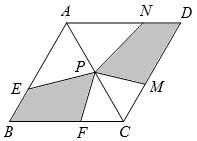
(1)求证:∠APE=∠CFP;
(2)设四边形CMPF的面积为S2,CF=x,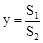 .
.
①求y关于x的函数解析式和自变量x的取值范围,并求出y的最大值;
②当图中两块阴影部分图形关于点P成中心对称时,求y的值.
(本题10分) 某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
(本题10分)阅读材料:小明在学习实数后,发现一些含根号的式子可以写成另一个式子的平方,如3+2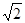 =(1+
=(1+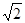 )
)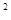 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b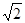 =(m+n
=(m+n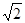 )
)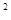 (其中a、b、m、n均为正整数),
(其中a、b、m、n均为正整数),
则有a+b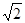 =m2+2n2+2mn
=m2+2n2+2mn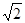 ,∴a= m2+2n2,b=2mn.
,∴a= m2+2n2,b=2mn.
这样小明就找到了一种把部分a+b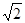 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b =(m+n
=(m+n )
)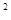 ,用含m、n的式子分别表示a、b,得:a=, b= ;
,用含m、n的式子分别表示a、b,得:a=, b= ;
(2)利用所探索的结论,找一组正整数a、b、m、n填空:+ =(+
=(+  )
)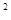 ;
;
(3)若a+4 =(m+n
=(m+n )
)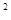 ,且a、m、n均为正整数,求a的值.
,且a、m、n均为正整数,求a的值.
(本题10分) 烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
(本题8分)如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB="DC" ;(2)试判断△OEF的形状,并说明理由.
(本题8分)已知y=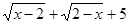 ,求
,求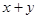 的算术平方根.
的算术平方根.