已知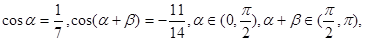 求
求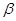 的值。
的值。
设命题p:实数x满足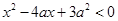 ,其中
,其中 ,命题
,命题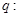 实数
实数 满足
满足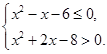 .
.
(1)若 且
且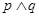 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是
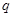 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
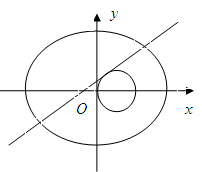
已知中心在坐标原点,焦点在 轴上的椭圆过点
轴上的椭圆过点 ,且它的离心率
,且它的离心率 .
.
(1)求椭圆的标准方程;
(2)与圆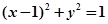 相切的直线
相切的直线 交椭圆于
交椭圆于 两点,若椭圆上一点
两点,若椭圆上一点 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.
已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
设命题p:f(x)= 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若 p∧q为真,试求实数m的取值范围.
p∧q为真,试求实数m的取值范围.