(本小题满分16分)
已知数列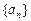 的前
的前 项和
项和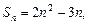 数列
数列 是正项等比数列,且
是正项等比数列,且 .
.
(1)求数列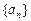 和
和 的通项公式;
的通项公式;
(2)记 ,是否存在正整数
,是否存在正整数 ,使得对一切
,使得对一切 ,都有
,都有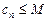 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
在△ABC中,角A、B、C所对的边分别是a、b、c,已知c=2,C=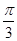 .
.
(1)若△ABC的面积等于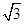 ,求a、b;
,求a、b;
(2)若sinC+sin(B-A)=2sin2A,求△ABC的面积.
在△ABC中,a、b、c分别是角A、B、C的对边,且 .
.
(1)求角B的大小;
(2)若b=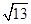 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
在△ABC中,a=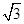 ,b=
,b=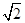 ,B=45°.求角A、C和边c.
,B=45°.求角A、C和边c.
设函数f(x)=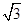 sinxcosx+cos2x+a.
sinxcosx+cos2x+a.
(1)写出函数f(x)的最小正周期及单调递减区间;
(2)当x∈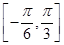 时,函数f(x)的最大值与最小值的和为
时,函数f(x)的最大值与最小值的和为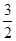 ,求a的值.
,求a的值.
设函数f(x)=(sinωx+cosωx)2+2cos2ωx(ω>0)的最小正周期为 .
.
(1)求ω的最小正周期;
(2)若函数y=g(x)的图象是由y=f(x)的图象向右平移 个单位长度得到,求y=g(x)的单调增区间.
个单位长度得到,求y=g(x)的单调增区间.