(本小题满分12分) 斜三棱柱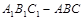 中,侧面
中,侧面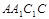
 底面ABC,侧面
底面ABC,侧面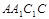 是菱形,
是菱形, ,
,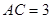 ,
, ,E、F分别是
,E、F分别是 ,AB的中点.
,AB的中点.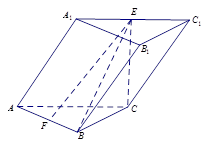
(1)求证:EF∥平面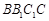 ;
;
(2)求证:CE⊥面ABC.
(3)求四棱锥 的体积.
的体积.
(本小题满分12分)
已知函数 在
在 和
和 处有极值。
处有极值。
(Ⅰ)求 的值;
的值;
(Ⅱ)求曲线 在
在 处的切线方程.
处的切线方程.
(本小题满分12分)
甲乙两位玩家在进行“石头、剪子、布”的游戏,假设两人在游戏时出示三种手势是等可能的。
(Ⅰ)求在1次游戏中甲胜乙的概率;
(Ⅱ)若甲乙双方共进行了3次游戏,随机变量 表示甲胜乙的次数,求
表示甲胜乙的次数,求 的分布列和数学期望.
的分布列和数学期望.
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵
 ,其中
,其中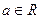 ,若点
,若点 在矩阵
在矩阵 的变换下得到点
的变换下得到点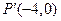 ,
,
(Ⅰ)求实数a的值;(Ⅱ)求矩阵 的特征值及其对应的特征向量.
的特征值及其对应的特征向量.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
已知直线的极坐标方程为 ,圆
,圆 的参数方程为
的参数方程为
(其中 为参数).
为参数).
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.
(本小题满分14分)
已知 ,
, ,
, .
.
(Ⅰ)当 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ)求 在点
在点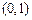 处的切线与直线
处的切线与直线 及曲线
及曲线 所围成的封闭图形的面积;
所围成的封闭图形的面积;
(Ⅲ)是否存在实数 ,使
,使 的极大值为3?若存在,求出
的极大值为3?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分13分)(1)已知a>0且a 1常数,求函数
1常数,求函数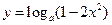 定义
定义
域和值域;
(2)已知命题P:函数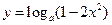 在
在 上单调递增;命题Q:不等式
上单调递增;命题Q:不等式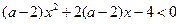 对任意实数
对任意实数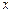 恒成立;若
恒成立;若 是真命题,求实数
是真命题,求实数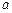 的取值范
的取值范
围