(本小题满分14分)已知数列 (
( ,
, )满足
)满足 ,
,  其中
其中 ,
, .
.
(1)当 时,求
时,求 关于
关于 的表达式,并求
的表达式,并求 的取值范围;
的取值范围;
(2)设集合 .
.
①若 ,
, ,求证:
,求证: ;
;
②是否存在实数 ,
, ,使
,使 ,
, ,
, 都属于
都属于 ?若存在,请求出实数
?若存在,请求出实数 ,
, ;若不存在,请说明理由.
;若不存在,请说明理由.
已知数列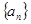 的前
的前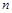 项和
项和 是二项式
是二项式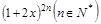 展开式中含
展开式中含 奇次幂的系数和.
奇次幂的系数和.
(1)求数列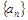 的通项公式;
的通项公式;
(2)设 ,求
,求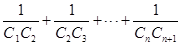 的值.
的值.
在平面直角坐标系 中,动点
中,动点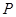 到两点
到两点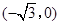 ,
,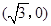 的距离之和等于
的距离之和等于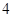 ,设点
,设点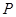 的轨迹为曲线
的轨迹为曲线 ,直线
,直线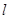 过点
过点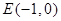 且与曲线
且与曲线 交于
交于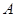 ,
,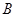 两点.
两点.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)是否存在△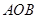 面积的最大值,若存在,求出△
面积的最大值,若存在,求出△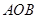 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
已知函数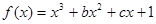 在区间
在区间 ,
,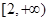 上单调递增,在区间[-2,2]上单调递减.
上单调递增,在区间[-2,2]上单调递减.
(1)求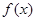 的解析式;
的解析式;
(2)设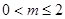 ,若对任意的x1、x2
,若对任意的x1、x2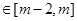 不等式
不等式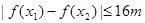 恒成立,求实数m的最小值。
恒成立,求实数m的最小值。
如图,已知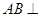 平面
平面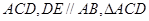 是正三角形,且
是正三角形,且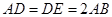 .
.
(1)设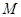 是线段
是线段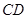 的中点,求证:
的中点,求证: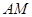 ∥平面
∥平面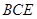 ;
;
(2)求直线 与平面
与平面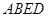 所成角的余弦值.
所成角的余弦值.
一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求:
(1)连续取两次都是红球的概率;
(2)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,但取球次数最多不超过4次,求取到黑球的概率。