在平面直角坐标系 中,动点
中,动点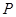 到两点
到两点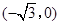 ,
,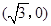 的距离之和等于
的距离之和等于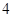 ,设点
,设点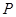 的轨迹为曲线
的轨迹为曲线 ,直线
,直线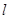 过点
过点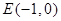 且与曲线
且与曲线 交于
交于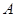 ,
,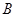 两点.
两点.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)是否存在△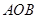 面积的最大值,若存在,求出△
面积的最大值,若存在,求出△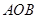 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
(本小题满分12分)已知椭圆C:
 的离心率为
的离心率为 ,长轴长为8.。
,长轴长为8.。
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若不垂直于坐标轴的直线 经过点P(m,0),与椭圆C交于A,B两点,设点Q的坐标为(n,0),直线AQ,BQ的斜率之和为0,求
经过点P(m,0),与椭圆C交于A,B两点,设点Q的坐标为(n,0),直线AQ,BQ的斜率之和为0,求 的值。
的值。
(本小题满分12分)某灯具厂分别在南方和北方地区各建一个工厂,生产同一种灯具(售价相同),为了了解北方与南方这两个工厂所生产得灯具质量状况,分别从这两个工厂个抽查了25件灯具进行测试,结果如下:
(Ⅰ)根据频率分布直方图,请分别求出北方、南方两个工厂灯具的平均使用寿命;
(Ⅱ)某学校欲采购灯具,同时试用了南北两工厂的灯具各两件,试用500小时后,若北方工厂生产的灯具还能正常使用的数量比南方工厂多,该学校就准备采购北方工厂的灯具,否则就采购南方工厂的灯具,试估计该学校采购北方工厂的灯具的概率。(视频率为概率)
(本小题满分 14 分)设数列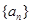 的首项
的首项 ,且
,且 ,
,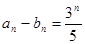 ,
,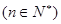 .
.
(Ⅰ)证明: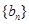 是等比数列;
是等比数列;
(Ⅱ)若 ,数列
,数列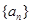 中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
(Ⅲ)若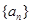 是递增数列,求
是递增数列,求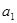 的取值范围.
的取值范围.
(本小题满分13分)已知函数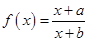 (
( 、
、 为常数).
为常数).
(Ⅰ)若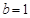 ,解不等式
,解不等式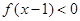 ;
;
(Ⅱ)若 ,当
,当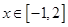 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)已知函数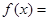
 ,(
,(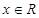 ).
).
(Ⅰ)求函数 的递增区间;
的递增区间;
(Ⅱ)若函数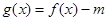 在
在 上有两个不同的零点
上有两个不同的零点 、
、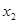 ,求
,求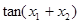 的值.
的值.