(本小题满分12分)已知椭圆C:
 的离心率为
的离心率为 ,长轴长为8.。
,长轴长为8.。
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若不垂直于坐标轴的直线 经过点P(m,0),与椭圆C交于A,B两点,设点Q的坐标为(n,0),直线AQ,BQ的斜率之和为0,求
经过点P(m,0),与椭圆C交于A,B两点,设点Q的坐标为(n,0),直线AQ,BQ的斜率之和为0,求 的值。
的值。
(.(本小题满分12分)
如图,焦距为2的椭圆E的两个顶点分别为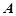 和
和 ,且
,且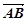 与
与 共线.
共线.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若直线 与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
((本小题满分12分)
数列 各项均为正数,其前
各项均为正数,其前 项和为
项和为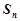 ,且满足
,且满足 .
.
(Ⅰ)求证数列 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)设 , 求数列
, 求数列 的前n项和
的前n项和 ,并求使
,并求使 对所
对所
有的 都成立的最大正整数m的值.
都成立的最大正整数m的值.
((本小题满分12分)
如图,在四棱锥 中,侧棱
中,侧棱 底面
底面 ,底面
,底面 为矩形,
为矩形, ,
, 为
为 的上一点,且
的上一点,且 ,
, 为PC的中点.
为PC的中点.
(Ⅰ)求证: 平面AEC;
平面AEC;
(Ⅱ)求二面角 的余弦值.
的余弦值.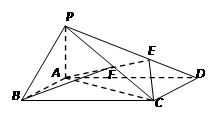
(本小题满分12分)
在某海岸A处,发现北偏东 方向,距离A处
方向,距离A处 n mile的B处有一艘走私船
n mile的B处有一艘走私船
在A处北偏西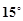 的方向,距离A处
的方向,距离A处 n mile的C处的缉私船奉命以
n mile的C处的缉私船奉命以 n mile/h的速度追截走私船. 此时,走私船正以5 n mile/h的速度从B处按照北偏东
n mile/h的速度追截走私船. 此时,走私船正以5 n mile/h的速度从B处按照北偏东 方向逃窜,问缉私船至少经过多长时间可以追上走私船,并指出缉私船航行方向.
方向逃窜,问缉私船至少经过多长时间可以追上走私船,并指出缉私船航行方向.
.(本小题满分10分)
记不等式组 表示的平面区域为M.
表示的平面区域为M.
(Ⅰ)画出平面区域M,并求平面区域M的面积;
(Ⅱ)若点 为平面区域M中任意一点,求直线
为平面区域M中任意一点,求直线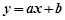 的图象经过一、二、四象限的概率.
的图象经过一、二、四象限的概率.