作图题：
如图，一块大的三角板ABC，D是AB上一点，现要求过点D割出一块小的角板ADE，使∠ADE=∠ABC，请用尺规作出∠ADE．（不写作法，保留作图痕迹，要写结论）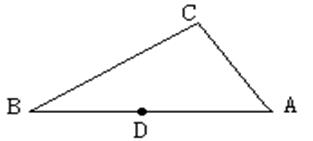
利用乘法公式简算（每小题4分，共16分）
（1）1102－109×111
（2）98
（3）（x+3y+2）（x—3y+2）
（4）化简求值：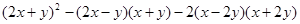
，其中
，
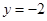
已知：∠MON=80°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O 重合），连接AC交射线OE于点D．设∠OAC=x°．
（1）如图1，若AB∥ON，则①∠ABO的度数是；②如图2，当∠BAD=∠ABD时，试求x的值（要说明理由）；
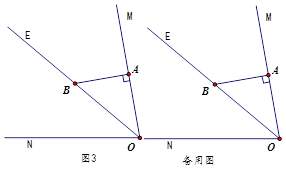
（2）如图3，若AB⊥OM，则是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，直接写出x的值；若不存在，说明理由．（自己画图）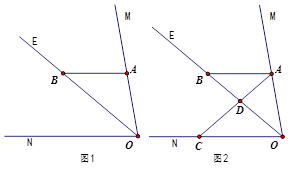
观察下表多项式分解因式的特征，并回答问题．
| 1 |
2 |
3 |
4 |
| 多项式 |
常数项 |
一次项系数 |
分解因式 |
 |
8=2×4 |
6=2+4 |
=（x+2）（x+4） |
 |
8=（-2）×（-4） |
-6=（-2）+（-4） |
=（x-2）（x-4） |
 |
-8=4×（-2） |
2=4+（-2） |
=（x+4）（x-2） |
对于二次项系数为1的二次三项式，若符合上述表中（2）（3）栏目的特征，就可以采用表中方法进行因式分解．
（1）分解因式：
；
（2）若
可分解为两个一次因式的积，则整数p的值有个；
先阅读下面的内容，再解决问题，
例题：若m2+2mn+2n2﹣6n+9=0，求m和n的值．
解：∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴（m+n）2+（n﹣3）2=0
∴m+n=0，n﹣3=0
∴m=﹣3，n=3
（1）若x2+2y2﹣2xy+4y+4=0，求xy的值．
（2）已知整数a、b、c是不等边△ABC的三边长，满足a2+b2=6a+8b﹣25，且c是△ABC中最长的边，求c的值．
