（本小题满分12分）如图,四边形ABCD是梯形,四边形CDE-优题课

（本小题满分12分）
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,
∠BAD＝∠CDA＝90°,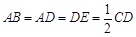,M是线段AE上的动点．

（1）试确定点M的位置,使AC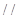平面DMF,并说明理由；
（2）在（1）的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值．

科目数学题型解答题难度中等

知识点：平行线法

已知函数 $f (x) = x^{3} + (1 - a) x^{2} - a (a + 2) x + b (a, b \in R)$ .

（Ⅰ）若函数 $f (x)$ 的图像过原点，且在原点处的切线斜率是-3，求a，b的值；

（Ⅱ）若函数 $f (x)$ 在区间 $(- 1, 1)$ 上不单调，求a的取值范围.

设 $S_{n}$ 为数列 ${a_{n}}$ 的前 n项和， $S_{n} = k n^{2} + n, n \in N^{*}$ ，其中 $k$ 是常数.

（Ⅰ）求 $a_{1}$ 及 $a_{n}$ ；

（Ⅱ）若对于任意的 $m \in N^{*}$ , $a_{m}$ , $a_{2 m}$ , $a_{4 m}$ 成等比数列，求 k的值.

如图， $DC ⊥ 平面 ABC$ , $EB ∥ DC$ , $AC = BC = EB = 2 DC = 2$ , $∠ ACB = 120 °$ ，P,Q分别为AE,AB的中点.

（Ⅰ）证明： $PQ ∥ 平面 ACD$ ；

（Ⅱ）求 $AD$ 与 $平面 ABE$ 所成角的正弦值.

在 $ΔABC$ 中，角A,B,C所对的边分别为a,b,c,且满足 $\cos \frac{A}{2} = \frac{2 \sqrt{5}}{5}$ ， $\vec{AB} \cdot \vec{AC} = 3$ .

(Ⅰ)求 $△ ABC$ 的面积；

（Ⅱ）若 $c = 1$ ，求 $a$ 的值.

双曲线 $C_{1} : \frac{x^{2}}{4^{2}} - \frac{y^{2}}{b^{2}} = 1$ ，圆 $C_{2} : x^{2} + y^{2} = 4 + b^{2} (b > 0)$ 在第一象限交点为A， $A (x_{A}, y_{A})$ ，曲线 $Γ \{\begin{matrix} \frac{x^{2}}{4} - \frac{y^{2}}{b^{2}} = 1, |x| > x_{A} \\ x^{2} + y^{2} = 4 + b^{2}, |x| > x_{A} \end{matrix}$ 。

（1）若 $x_{A} = \sqrt{6}$ ，求b；

（2）若 $b = \sqrt{5}$ ， $C_{2}$ 与x轴交点记为 $F_{1} 、 F_{2}$ ，P是曲线 $Γ$ 上一点，且在第一象限，并满足 $|P F_{1}| = 8$ ，求∠ $F_{1} P F_{2}$ ；

（3）过点 $S (0, 2 + \frac{b^{2}}{2})$ 且斜率为 $- \frac{b}{2}$ 的直线 $l$ 交曲线 $Γ$ 于M、N两点，用b的代数式表示 $\vec{OM} ∙ \vec{ON}$ ，并求出 $\vec{OM} ∙ \vec{ON}$ 的取值范围。

试卷网试题网古诗词网作文网范文网