(本题6分)先阅读下面的内容,再解决问题,
例题:若 ,求
,求 和
和 的值.
的值.
解:∵
∴
∴
∴ ,
,
∴ ,
,
问题:
(1)若△ABC的三边长 都是正整数,且满足
都是正整数,且满足 ,请问△ABC是什么形状?
,请问△ABC是什么形状?
(2)已知 是△ABC的三边长,
是△ABC的三边长, 是△ABC的最短边且满足
是△ABC的最短边且满足 ,求
,求 的范围.
的范围.
学校6名教师和234名学生集体外出活动,准备租用445座大客车或30座小客车,若租用1辆大车2辆小车供需租车费1000元;若若租用2辆大车1辆小车供需租车费1100元.
(1)求大、小车每辆的租车费各是多少元?
(2)若每辆车上至少要有一名教师,且总租车费用不超过2300元,求最省钱的租车方案。
矩形ABCD中,AB=2AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
(1)求证:⊿AEF∽⊿DCE
(2)求tan∠ECF的值.
关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
如图,等腰梯形ABCD中,AD∥BC,点E是AD延长线上的一点,且CE=CD,求证:∠B=∠E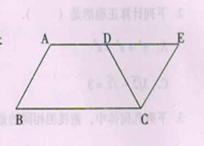
在一个口袋中有4个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸取一个小球然后放回,再随机地摸出一个小球,求下列事件的概率:
(1)两次取的小球的标号相同
(2)两次取的小球的标号的和等于4