(5分) 解不等式组：
(6分)如图，点B、D、C、F在一条直线上，且BC = FD，AB = EF.
（1）请你只添加一个条件（不再加辅助线），使△ABC≌△EFD，你添加的条件是；
（2）添加了条件后，证明△ABC≌△EFD.
(5分) 计算：
如图9，已知直线
的解析式为
，它与
轴、
轴分别相交于
、
两点，平行于直线的直线
从原点
出发，沿轴正方向以每秒
个单位长度的速度运动，运动时间为
秒，运动过程中始终保持
，直线与轴，轴分别相交于
、
两点，线段
的中点为
，以为圆心，以为直径在上方作半圆，半圆面积为
，当直线与直线重合时，运动结束．
求、两点的坐标；
求与的函数关系式及自变量的取值范围；
直线在运动过程中，
当为何值时，半圆与直线相切？
是否存在这样的值，使得半圆面积
？若存在，求出值，若不存在，说明理由．
在如图8所示的方格图中，每个小正方形的顶点称为“格点”，且每个小正方形的边长均为1个长度单位，以格点为顶点的图形叫做“格点图形”，根据图形解决下列问题：
图中格点
是由格点
通过怎样变换得到的？
如果建立直角坐标系后，点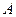
的坐标为（
，
），点
的坐标为
，请求出过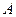点的正比例函数的解析式，并写出图中格点
各顶点的坐标．
-2013×2011-1