如图9，已知直线
的解析式为
，它与
轴、
轴分别相交于
、
两点，平行于直线的直线
从原点
出发，沿轴正方向以每秒
个单位长度的速度运动，运动时间为
秒，运动过程中始终保持
，直线与轴，轴分别相交于
、
两点，线段
的中点为
，以为圆心，以为直径在上方作半圆，半圆面积为
，当直线与直线重合时，运动结束．
求、两点的坐标；
求与的函数关系式及自变量的取值范围；
直线在运动过程中，
当为何值时，半圆与直线相切？
是否存在这样的值，使得半圆面积
？若存在，求出值，若不存在，说明理由．
已知抛物线与 轴交于 、 ， 两点，与 轴交于点 ，过抛物线上点 作 轴于点 ，连接 ．
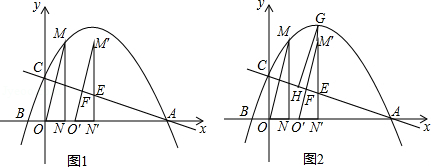
（1）求此抛物线的解析式；
（2）如图1，将 沿 轴向右平移 个单位 到△ 的位置， 、 与直线 分别交于点 、 ．
①当点 为 的中点时，求 的值；
②如图2，若直线 与抛物线相交于点 ，过点 作 交 于点 ，试确定线段 是否存在最大值？若存在，求出它的最大值及此时 的值；若不存在，请说明理由．
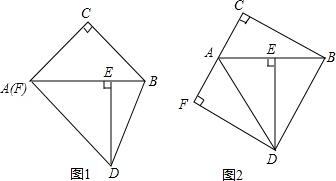
在 中， ， 绕点 顺时针旋转到 的位置，点 在斜边 上，连接 ，过点 作 于点 ．
（1）如图1，若点 与点 重合，求证： ；
（2）若 ，
①如图2，当点 在线段 的延长线上时，判断线段 与线段 的数量关系，并说明理由；
②当点 在线段 上时，设 ，请用含 的代数式表示线段 ．
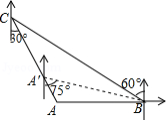
如图，“中国海监50”正在南海海域 处巡逻，岛礁 上的中国海军发现点 在点 的正西方向上，岛礁 上的中国海军发现点 在点 的南偏东 方向上，已知点 在点 的北偏西 方向上，且 、 两地相距120海里．
（1）求出此时点 到岛礁 的距离；
（2）若“中海监50”从 处沿 方向向岛礁 驶去，当到达点 时，测得点 在 的南偏东 的方向上，求此时“中国海监50”的航行距离．（注 结果保留根号）
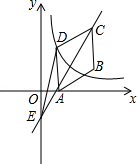
如图，在平行四边形 中，点 、 、 的坐标分别是 、 、 ，双曲线 过点 ．
（1）求双曲线的解析式；
（2）作直线 交 轴于点 ，连接 ，求 的面积．
如图，在 中，点 是直径 延长线上一点，过点 作 的切线，切点为 ，连接 ．
（1）求证： ；
（2）若 平分 ，且分别交 、 于点 、 ，当 时，求 的长．
