(本题8分)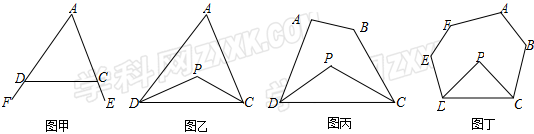
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
如图甲,∠FDC、∠ECD为△ADC的两个外角,则∠A与∠FDC+∠ECD的数量关系 .
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
如图乙,在△ADC中,DP、CP分别平分∠ADC和∠ACD,则∠P与∠A的数量关系 .
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图丙,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,则∠P与∠A+∠B的数量关系 .
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?如图丁
则∠P与∠A+∠B+∠E+∠F的数量关系 .
探究五:如图,四边形ABCD中,∠F为四边形ABCD的∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的锐角,若设∠A=α,∠D=β;
(1)如图①,α+β>180°,则∠F= ;(用α,β表示)
(2)如图②,α+β<180°,请在图中画出∠F,且∠F= ;(用α,β表示)
(3)一定存在∠F吗?如有,直接写出∠F的值,如不一定,直接指出α,β满足什么条件时,不存在∠F.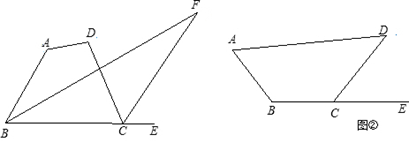
先化简再求值: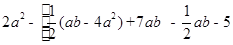 ,其中
,其中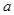 =2b
=2b
在数轴上表示下列各数:0,–4.2,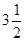 ,–2,+7,
,–2,+7,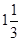 ,并用“<”号连接
,并用“<”号连接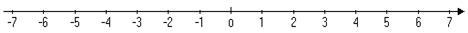
化简
(1)-5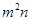 +4m
+4m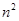 -2mn+6
-2mn+6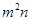 +3mn
+3mn
(2)2(2a-3b)-3(2b-3a)
如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.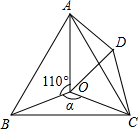
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.
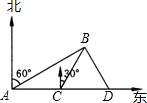
如图所示,某船上午11时30分在A处观测海岛B在北偏东60°方向,该船以每小时10海里的速度航行到C处,再观测海岛B在北偏东30°方向,又以同样的速度继续航行到D处,再观测海岛在北偏西30°方向,当轮船到达C处时恰好与海岛B相距20海里,请你确定轮船到达C处和D处的时间.