如图,直线 与反比例函数
与反比例函数 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.
(1)求该反比例函数的表达式;
(2)若P为y轴上的点,且△AOP的面积是△AOB的面积的 ,请求出点P的坐标.
,请求出点P的坐标.
(3)写出直线 向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标。
向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标。
先化简,再求值: ,其中
,其中 .
.
﹣(本题12分)已知二次函数y=x2+bx+c与x轴交于A(-1,0)、B(1,0)两点.
(1)求这个二次函数的关系式;
(2)若有一半径为r的⊙P,且圆心P在抛物线上运动,当⊙P与两坐标轴都相切时,求半径r的值.
(3)半径为1的⊙P在抛物线上,当点P的纵坐标在什么范围内取值时,⊙P与y轴相离、相交?
﹣(本题12分)甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.
(1)写出乙船在逆流中行驶的速度.
(2)求甲船在逆流中行驶的路程.
(3)求甲船到A港的距离y1与行驶时间x之间的函数关系式.
(4)求救生圈落入水中时,甲船到A港的距离.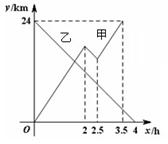 【参考公式:船顺流航行的速度
【参考公式:船顺流航行的速度 船在静水中航行的速度+水流速度,船逆流航行的速度
船在静水中航行的速度+水流速度,船逆流航行的速度 船在静水中航行的速度
船在静水中航行的速度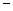 水流速度.】
水流速度.】
﹣(本题12分)在一平直河岸 同侧有
同侧有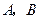 两个村庄,
两个村庄,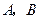 到
到 的距离分别是3km和2km,
的距离分别是3km和2km,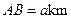
 .现计划在河岸
.现计划在河岸 上建一抽水站
上建一抽水站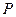 ,用输水管向两个村庄供水.
,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图(1)是方案一的示意图,设该方案中管道长度为 ,且
,且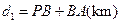 (其中
(其中 于点
于点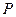 );图(2)是方案二的示意图,设该方案中管道长度为
);图(2)是方案二的示意图,设该方案中管道长度为 ,且
,且 (其中点
(其中点 与点
与点 关于
关于 对称,
对称, 与
与 交于点
交于点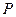 ).
).
 |
(1)观察计算
在方案一中,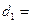 km(用含
km(用含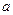 的式子表示);
的式子表示);
在方案二中,组长小宇为了计算 的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算,
的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算, km(用含
km(用含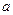 的式子表示).
的式子表示).
(2)探索归纳
①当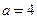 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
当 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”); ②请你参考右边方框中的方法指导,
②请你参考右边方框中的方法指导,
就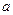 (当
(当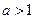 时)的所有取值情况进
时)的所有取值情况进
行分析,要使铺设的管道长度较短,
应选择方案一还是方案二?
﹣(本题10分)已知: 如图, AB是⊙O的直径,⊙O过AC的中点D, DE切⊙O于点D, 交BC于点E. 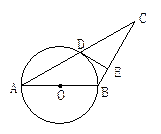
(1)求证: DE⊥BC;
(2)如果CD=4,CE=3,求⊙O的半径.