如图，正方形AOCB在平面直角坐标系xoy中，点O为原点，点B在反比例函数
（x＞0）图象上，△BOC的面积为8．
（1）求反比例函数
的关系
（2）若动点E从A开始沿AB向B以每秒1个单位的速度运动，同时动点F从B开始沿BC向C以每秒2个单位的速度运动，当其中一个动点到达端点时，另一个动点随之停止运动．若运动时间用t表示，△BEF的面积用S表示，求出S关于t的函数关系式？
（3）当运动时间为
秒时，在坐标轴上是否存在点P，使△PEF的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．
如图，已知∠A＝∠F，∠C＝∠D.试问BD是否与CE平行?为什么?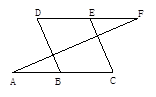
如图，已知AC⊥BC，CD⊥AB，DE⊥AC，∠1与∠2互补，判断HF与AB是否垂直，
并说明理由（填空）．
解：垂直。理由如下：
∵DE⊥AC，AC⊥BC
∴∠AED=∠ACB=90º（垂直的意义）
∴DE∥BC（ ）
∴∠1=∠DCB（ ）
∵∠1与∠2互补（已知）
∴∠DCB与∠2互补
∴______∥_______（ ）
∴____________＝∠CDB（ ）
∵CD⊥AB
∴∠CDB=90º
∴∠HFB="90º"
∴HF⊥AB
已知AB为⊙O的直径，PA、PC是⊙O的切线，A、C为切点，∠BAC＝30°．求∠P的度数；
若AB＝2，求PA的长．
如图，
是⊙
的切线，
为切点，
是⊙的弦，过作
于点
．若
，
，
．求⊙
的半径；求AC的值．
长沙市某楼盘准备以每平方米5000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望．为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米4050元的均价开盘销售．求平均每次下调的百分率．