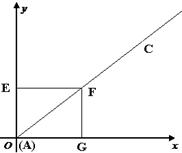
请阅读下列材料:让我们来规定一种运算: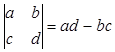 ,例如:
,例如: =2×5-3×4=10-12=-2. 按照这种运算的规定,若
=2×5-3×4=10-12=-2. 按照这种运算的规定,若 =
= ,试用方程的知识求x的值。
,试用方程的知识求x的值。
如图,平行于y轴的直尺(一部分)与双曲线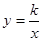 (
( )交于点
)交于点 、
、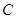 ,与
,与 轴交于点
轴交于点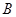 、
、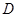 ,连结
,连结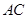 ,
,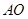 ,
, 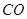 ,点
,点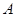 、
、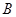 的刻度分别为5、2(单位:
的刻度分别为5、2(单位: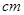 ),直尺的宽度为
),直尺的宽度为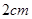 ,
,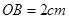 .
.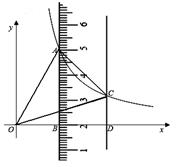
(1)试求反比例函数的解析式和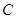 点的坐标;
点的坐标;
(2)试求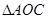 的面积.
的面积.
如图,在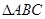 中,
中,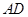 是边
是边 上的中线,过点
上的中线,过点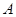 作
作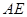 ∥
∥ ,过
,过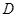 作
作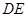 ∥
∥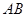 ,
,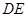 与
与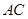 、
、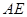 分别交于点
分别交于点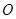 、点
、点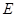 ,连接
,连接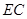 .
.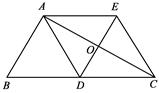
(1)求证: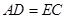 ;
;
(2)当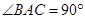 时,求证:四边形
时,求证:四边形 是菱形.
是菱形.
“十年树木,百年树人”,教师的素养关系到国家的未来.我市某区招聘美术教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并按2∶3∶5的比例折合纳入总分,最后,按照成绩的排序从高到低依次录取.该区要招聘2名美术教师,通过笔试、专业技能测试筛选出前6名选手进入说课环节,这6名选手的各项成绩见下表:
| 序号 |
1 |
2 |
3 |
4 |
5 |
6 |
| 笔试成绩 |
66 |
90 |
65 |
64 |
86 |
84 |
| 专业技能测试成绩 |
95 |
92 |
88 |
80 |
93 |
92 |
| 说课成绩 |
85 |
78 |
94 |
88 |
86 |
85 |
(1)笔试成绩的极差是多少?
(2)写出说课成绩的中位数、众数;
(3)已知序号为1,2,3,4号选手的成绩分别为84.2分,84.6分,86.4分,80.8分,请你判断这六位选手中序号是多少的选手将被录用?为什么?
化简: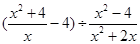 .
.
如图,以矩形ABCD的顶点A为原点,AD所在的直线为x轴,AB所在的直线为y轴,建立平面直角坐标系.点D的坐标为(8,0),点B的坐标为(0,6),点F在对角线AC上运动(点F不与点A、C重合),过点F分别作x轴、y轴的垂线,垂足为G、E.设四边形BCFE的面积为S1,四边形CDGF的面积为S2,△AFG的面积为S3.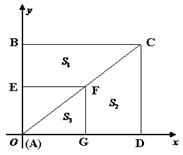
(1)试判断S1、S2,的关系,并加以证明;
(2)当S3:S1=1:3时,求点F的坐标;
(3)如图,在(2)的条件下,把△AEF沿对角线AC所在直线平移,得到△A’E’F’,且A’、F’两点始终在直线AC上,是否存在这样的点E’,使点E’到x轴的距离与到y轴的距离比是5:4.若存在,请求出点E’的坐标;若不存在,请说明理由.