已知抛物线的顶点在坐标原点,焦点在 轴上,且过点
轴上,且过点 .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)直线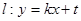 ,与圆
,与圆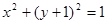 相切且与抛物线交于不同的两点
相切且与抛物线交于不同的两点 ,当
,当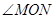 为直角时,求△OMN的面积。
为直角时,求△OMN的面积。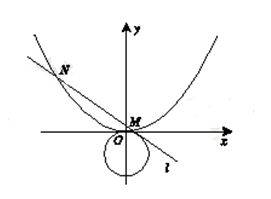
已知椭圆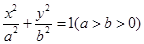 的右焦点为
的右焦点为 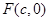 ,
,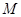 为椭圆的上顶点,
为椭圆的上顶点,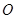 为坐标原点,且两焦点和短轴的两端构成边长为
为坐标原点,且两焦点和短轴的两端构成边长为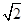 的正方形.
的正方形.
(1)求椭圆的标准方程;
(2)是否存在直线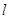 交与椭圆于
交与椭圆于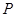 ,
, 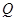 ,且使
,且使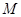 ,使得
,使得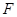 为
为 的垂心,若存在,求出
的垂心,若存在,求出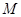 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
设数列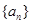 的前
的前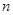 项和为
项和为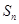 ,且满足
,且满足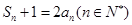 .
.
(1)求数列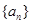 的通项公式;
的通项公式;
(2)在数列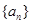 的每两项之间按照如下规则插入一些数后,构成新数列:
的每两项之间按照如下规则插入一些数后,构成新数列: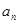 与
与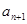 两项之间插入
两项之间插入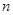 个数,使这
个数,使这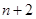 个数构成等差数列,其公差为
个数构成等差数列,其公差为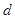 ,求数列
,求数列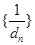 的前
的前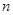 项和为
项和为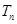 .
.
如图,直三棱柱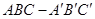 的侧棱长为3,
的侧棱长为3,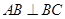 ,且
,且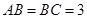 ,
,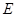 、
、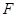 分别是棱
分别是棱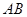 、
、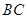 上的动点,且
上的动点,且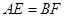
(1)证明:无论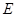 在何处,总有
在何处,总有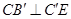 ;
;
(2)当三棱柱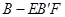 .的体积取得最大值时,求异面直线
.的体积取得最大值时,求异面直线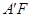 与
与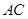 所成角的余弦值.
所成角的余弦值.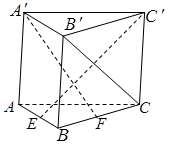
已知向量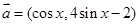 ,
, ,
,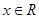 ,设函数
,设函数 .
.
(1)求函数 的最大值;
的最大值;
(2)在 中,角
中,角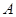 为锐角,角
为锐角,角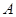 、
、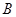 、
、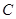 的对边分别为
的对边分别为 、
、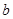 、
、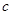 ,
,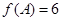 ,且
,且 的面积为3,
的面积为3,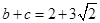 ,求
,求 的值.
的值.
已知函数 ,且
,且 在
在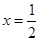 处的切线方程为
处的切线方程为 .
.
(1)求 的解析式;
的解析式;
(2)证明:当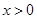 时,恒有
时,恒有 ;
;
(3)证明:若 ,
, ,且
,且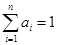 ,则
,则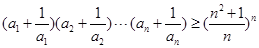 .
.