甲、乙两地相距12km.A车、B车先后从甲地出发匀速驶向乙地.A车从甲地到乙地需行驶15min;B车从甲地到乙地需行驶10min.若B车比A车晚出发2min:
(1)分别写出A、B两车所行路程关于A车行驶时间的函数关系式;
(2) A、B两车何时在途中相遇?相遇时距甲地多远?
(本小题满分13分)我国东部某风景区内住着一个少数民族部落,该部落拟投资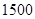 万元用于修复和加强民俗文化基础设施.据测算,修复好部落民俗文化基础设施后,任何一个月(每月均按
万元用于修复和加强民俗文化基础设施.据测算,修复好部落民俗文化基础设施后,任何一个月(每月均按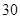 天计算)中第
天计算)中第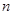 天的游客人数
天的游客人数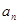 近似满足
近似满足 (单位:千人),第
(单位:千人),第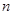 天游客人均消费金额
天游客人均消费金额 近似满足
近似满足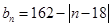 (单位:元).
(单位:元).
(1)求该部落第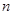 天的日旅游收入
天的日旅游收入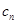 (单位:千元,
(单位:千元,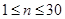 ,
,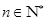 )的表达式;
)的表达式;
(2)若以一个月中最低日旅游收入金额的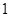 %作为每一天应回收的投资成本,试问该部落至少经过几年就可以收回全部投资成本.
%作为每一天应回收的投资成本,试问该部落至少经过几年就可以收回全部投资成本.
本小题满分13分)已知椭圆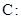
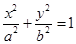 (
(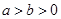 )的右焦点与抛物线
)的右焦点与抛物线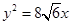 的焦点重合,且椭圆
的焦点重合,且椭圆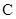 的离心率
的离心率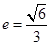 .
.
(1)求椭圆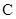 的标准方程;
的标准方程;
(2)若直线 (
( )与椭圆
)与椭圆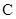 交于不同的两点
交于不同的两点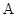 ,
,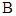 ,以线段
,以线段 为直径作圆
为直径作圆 .若圆
.若圆 与
与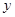 轴相切,求直线
轴相切,求直线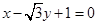 被圆
被圆 所截得的弦长.
所截得的弦长.
(本小题满分13分)某同学用“五点法”画函数 在某一个周期的图象时,列表并填入的部分数据如下表:
在某一个周期的图象时,列表并填入的部分数据如下表:
(1)求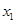 ,
, ,
, 的值及函数
的值及函数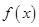 的表达式;
的表达式;
(2)将函数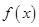 的图象向左平移
的图象向左平移 个单位,可得到函数
个单位,可得到函数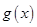 的图象,求函数
的图象,求函数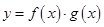 在区间
在区间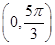 的最小值.
的最小值.
(本小题共13分)已知函数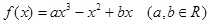 ,
,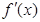 为其导函数,且
为其导函数,且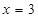 时
时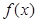 有极小值
有极小值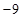 .
.
(Ⅰ)求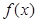 的单调递减区间;
的单调递减区间;
(Ⅱ)若不等式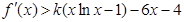 (为正整数)对任意正实数恒成立,求的最大值.(解答过程可参考使用以下数据:
(为正整数)对任意正实数恒成立,求的最大值.(解答过程可参考使用以下数据: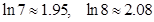 )
)
(本小题共14分)已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为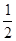 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设直线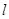 经过点
经过点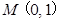 ,且与椭圆
,且与椭圆 交于
交于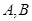 两点,若
两点,若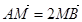 ,求直线
,求直线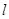 的方程.
的方程.