如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.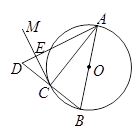
(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使CD = BC,连接AD与CM交于点E,若⊙O的半径为2,ED =1,求AC的长.
解方程:
如图,一次函数的图象与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,如果A点的坐标为(2,0),点C、D分别在第一、三象限,且OA=OB=AC=BD,试求一次函数和反比例函数的解析式.
反比例函数y=- 与直线y=-x+2的图象交于A、B两点,点A、B分别在第四、二象限,求:
与直线y=-x+2的图象交于A、B两点,点A、B分别在第四、二象限,求:
(1)A、B两点的坐标;
(2)△ABO的面积.
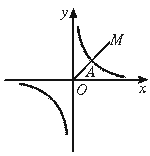
如图,第一象限的角平分线OM与反比例函数的图象相交于点A,已知OA=2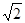 .
.
(1)求点A的坐标;
(2)求此反比例函数的解析式.
水池中有水若干吨,若单开一个出水口,水流速v与全池水放光所用时t如下表:
| 用时t(小时) |
10 |
5 |
 |
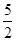 |
2 |
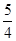 |
1 |
| ——……→逐渐减少 |
|||||||
| 出水速度乙(吨/小时) |
1 |
2 |
3 |
4 |
5 |
8 |
10 |
| ——……→逐渐增大 |
①写出放光池中水用时t(小时)与放水速度v(吨/小时)之间的函数关系.
②这是一个反比例函数吗?