黄商超市以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件.超市为增加销售量，决定降价销售，根据市场调查，单价第降低1元，可多售出10件，但最低单价应高于购进的价格；第二个月结束后，超市将对剩余的T恤一次性清仓销售，清仓时单价为40元，设第二个月单价降低x元.
（1）完成下表（不化简）
| 时间 |
第一个月 |
第二个月 |
清仓时 |
| 单价（元） |
80 |
|
40 |
| 销售量（件） |
200 |
|
|
（2）如果超市希望通过销售这批T恤获利9000元，那么第二个月的单价是多少元？
先化简，再求值： 
，其中
若关于x的二次函数y=a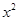
+bx+c（a＞0，c＞0，a、b、c是常数）与x轴交于两个不同的点A（
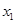，0），B（
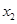，0）（0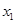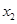＜＜），与y轴交于点P，其图像顶点为点M，点O为坐标原点。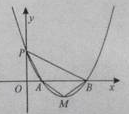
（1）当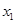=c=2，a=
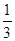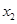时，求与b的值；
（2）当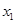=2c时，试问△ABM能否为等边三角形？判断并证明你的结论；
（3）当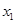=mc（m＞0）时，记△MAB，△PAB的面积分别为S1，S2，若△BPO∽△PAO，且S1=S2,求m的值。
|
在直角坐标系中，我们不妨将横坐标，纵坐标均为整数的点称之为“中国结”。
（1）求函数y=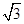
x+2的图像上所有“中国结”的坐标；
（2）求函数y=
（k≠0，k为常数）的图像上有且只有两个“中国结”，试求出常数k的值与相应“中国结”的坐标；
（3）若二次函数y=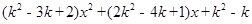
（k为常数）的图像与x轴相交得到两个不同的“中国结”，试问该函数的图像与x轴所围成的平面图形中（含边界），一共包含有多少个“中国结”？
如图，在直角坐标系中，⊙M经过原点O（0,0），点A（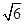
，0）与点B（0，－
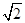），点D在劣弧OA上，连接BD交x轴于点C，且∠COD=∠CBO。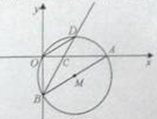
（1）求⊙M的半径；
（2）求证：BD平分∠ABO；
（3）在线段BD的延长线上找一点E，使得直线AE恰为⊙M的切线，求此时点E的坐标。
现代互联网技术的广泛应用，催生了快递行业的高速发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件。现假定该公司每月的投递总件数的增长率相同：
（1）求该快递公司投递快递总件数的月平均增长率；
（2）如果平均每人每月最多可投递快递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？