为鼓励大学毕业生自主创业，某市政府出台了相关政策：由政府协调-优题课

如图，在 $6 \times 4$ 的方格纸 $ABCD$ 中，请按要求画格点线段（端点在格点上），且线段的端点均不与点 $A$ ， $B$ ， $C$ ， $D$ 重合．

（1）在图1中画格点线段 $EF$ ， $GH$ 各一条，使点 $E$ ， $F$ ， $G$ ， $H$ 分别落在边 $AB$ ， $BC$ ， $CD$ ， $DA$ 上，且 $EF = GH$ ， $EF$ 不平行 $GH$ ．

（2）在图2中画格点线段 $MN$ ， $PQ$ 各一条，使点 $M$ ， $N$ ， $P$ ， $Q$ 分别落在边 $AB$ ， $BC$ ， $CD$ ， $DA$ 上，且 $PQ = \sqrt{5} MN$ ．

$A$ ， $B$ 两家酒店规模相当，去年下半年的月盈利折线统计图如图所示．

（1）要评价这两家酒店 $7 ~ 12$ 月的月盈利的平均水平，你选择什么统计量？求出这个统计量．

（2）已知 $A$ ， $B$ 两家酒店 $7 ~ 12$ 月的月盈利的方差分别为1.073（平方万元），0.54（平方万元）．根据所给的方差和你在（1）中所求的统计量，结合折线统计图，你认为去年下半年哪家酒店经营状况较好？请简述理由．

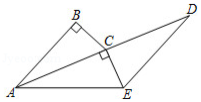
如图，在 $ΔABC$ 和 $ΔDCE$ 中， $AC = DE$ ， $∠ B = ∠ DCE = 90 °$ ，点 $A$ ， $C$ ， $D$ 依次在同一直线上，且 $AB / / DE$ ．

（1）求证： $ΔABC ≅ ΔDCE$ ．

（2）连结 $AE$ ，当 $BC = 5$ ， $AC = 12$ 时，求 $AE$ 的长．

（1）计算： $\sqrt{4} - | - 2 | + {(\sqrt{6})}^{0} - (- 1)$ ．

（2）化简： ${(x - 1)}^{2} - x (x + 7)$ ．

用各种盛水容器可以制作精致的家用流水景观（如图 $1)$ ．

科学原理：如图2，始终盛满水的圆柱体水桶水面离地面的高度为 $H$ （单位： $cm)$ ，如果在离水面竖直距离为 $h$ （单位： $cm)$ 的地方开大小合适的小孔，那么从小孔射出水的射程（水流落地点离小孔的水平距离） $s$ （单位： $cm)$ 与 $h$ 的关系式为 $s^{2} = 4 h (H - h)$ ．

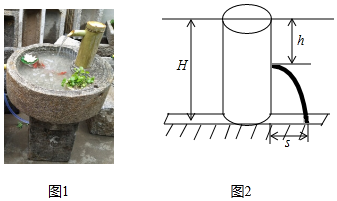
应用思考：现用高度为 $20 cm$ 的圆柱体塑料水瓶做相关研究，水瓶直立地面，通过连续注水保证它始终盛满水，在离水面竖直距离 $hcm$ 处开一个小孔．

（1）写出 $s^{2}$ 与 $h$ 的关系式；并求出当 $h$ 为何值时，射程 $s$ 有最大值，最大射程是多少？

（2）在侧面开两个小孔，这两个小孔离水面的竖直距离分别为 $a$ ， $b$ ，要使两孔射出水的射程相同，求 $a$ ， $b$ 之间的关系式；

（3）如果想通过垫高塑料水瓶，使射出水的最大射程增加 $16 cm$ ，求垫高的高度及小孔离水面的竖直距离．