(本题满分12分)
在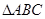 中,已知角
中,已知角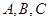 的对边分别为
的对边分别为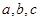 ,且
,且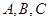 成等差数列.
成等差数列.
(1)若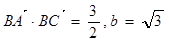 ,求
,求 的值;
的值;
(2)求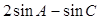 的取值范围.
的取值范围.
(14分)某工厂在试验阶段大量生产一种零件,这种零件有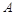 、
、 两项技术指标需要检测,设各项技术指标达标与否互不影响.若仅有A项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若仅有A项技术指标达标的概率为 ,A、B两项技术指标都不达标的概率为
,A、B两项技术指标都不达标的概率为 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率?
(2)若任意抽取该种零件4个,设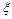 表示其中合格品的个数,求
表示其中合格品的个数,求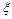 的分布列及数学期望
的分布列及数学期望 .
.
已知函数 (
( ).
).
(1)求函数 的最小正周期及
的最小正周期及 在区间
在区间 上的值域;
上的值域;
(2)在 中,
中, ,
, .若
.若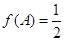 ,求
,求 的面积.
的面积.
(本小题满分10分)选修4-1:几何证明选讲
如图, 是
是 的一条切线,切点为
的一条切线,切点为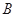 ,直线
,直线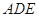 ,
,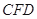 ,
,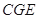 都是
都是 的割线,已知
的割线,已知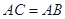 .
.
(Ⅰ)求证: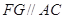 ;
;
(II)若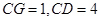 ,求
,求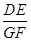 的值.
的值.
(本小题满分10分)选修4-5:不等式选讲
已知函数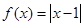 .
.
(Ⅰ)解不等式: 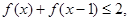 ;
;
(Ⅱ)若 ,求证:
,求证: ≤
≤ .
.
(本小题满分10分)选修4—4:坐标系与参数方程
已知点,参数,点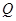 在曲线
在曲线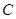 :上.
:上.
(Ⅰ)求在直角坐标系中点 的轨迹方程和曲线
的轨迹方程和曲线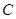 的方程;
的方程;
(Ⅱ)求 的最小值.
的最小值.