(本小题满分13分)
某大学志愿者协会有10名同学,成员构成如下表,其中表中部分数据不清楚,只知道从这10名同学中随机抽取一位,抽到该名同学为“数学专业”的概率为 .
.
| 专业 性别 |
中文 |
英语 |
数学 |
体育 |
| 男 |
 |
1 |
 |
1 |
| 女 |
1 |
1 |
1 |
1 |
现从这10名同学中随机选取3名同学参加社会公益活动(每位同学被选到的可能性相同).
(Ⅰ)求 的值;
的值;
(Ⅱ)求选出的3名同学恰为专业互不相同的男生的概率;
(Ⅲ)设 为选出的3名同学中“女生或数学专业”的学生的人数,求随机变量
为选出的3名同学中“女生或数学专业”的学生的人数,求随机变量 的分布列及其数学期望
的分布列及其数学期望 .
.
(本小题满分10分)选修4-5:不等式选讲
已知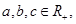 且
且 .证明:
.证明:
(Ⅰ)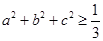 ;
;
(Ⅱ) .
.
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线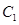 :
: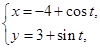 (
(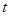 为参数),
为参数),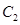 :
: (
( 为参数).
为参数).
(Ⅰ)化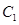 ,
,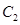 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若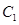 上的点
上的点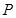 对应的参数为
对应的参数为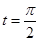 ,
,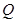 为
为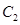 上的动点,求
上的动点,求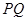 中点
中点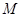 到直线
到直线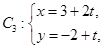 (
(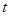 为参数)距离的最小值.
为参数)距离的最小值.
(本小题满分10分)选修4-1:几何证明选讲
已知 为圆
为圆 上的四点,直线
上的四点,直线 为圆
为圆 的切线,
的切线, ,
, 与
与 相交于
相交于 点.
点.
(Ⅰ)求证: 平分
平分 .
.
(Ⅱ)若 求
求 的长.
的长.
(本小题满分12分)
已知函数 ,函数
,函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)讨论 的单调性;
的单调性;
(Ⅱ)若 ,使得不等式
,使得不等式 成立,试求实数
成立,试求实数 的取值范围;
的取值范围;
(Ⅲ)当 时,对于
时,对于 ,求证:
,求证: .
.
(本小题满分12分)
已知 是公差为
是公差为 的等差数列,它的前
的等差数列,它的前 项和为
项和为 ,且
,且 .
.
(Ⅰ)求公差 的值;
的值;
(Ⅱ)若 ,
, 是数列
是数列 的前
的前 项和,不等式
项和,不等式 对所有的
对所有的 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值.