（本小题满分12分）
已知函数
，函数
，其中
为自然对数的底数．
（Ⅰ）讨论
的单调性；
（Ⅱ）若
，使得不等式
成立，试求实数
的取值范围；
（Ⅲ）当
时，对于
，求证：
．
已知函数
（1）在给定的直角坐
标系
内画出
的图象；
（2）写出的单调递增区间（不需要证明）；
（3）写出的最大值和最小值（不需要证明）
已知集合
，
，求：
(1) 
；
（2）
.
．对于定义域为[
0，1]的函数f(x)，如果同时满足以下三条：①对任意的x∈[0,1] ，总有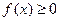
；②f(1)=1；③若
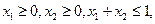都有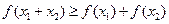
成立，则称函数f(x)为理想函数。
（1）若函数f(x)为理想函数，求f(0)的值；
（2）判断函数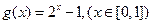
是否为理想函数，并予以证明。
已知函数
在
时都取得极值。
（1）求a、b的值；
（2）若对
恒成立，求c的取值范围。
已知△ABC的三个内角A、B、C成等差数列，求证：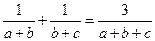
（a、b、c分别为角A、B、C的对边）。