（本小题满分12分）某商区停车场临时停车按时段收费，收费标准为：每辆汽车一次停车不超过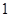
小时收费
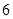元，超过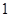小时的部分每小时收费
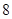元（不足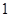小时的部分按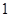小时计算）．现有甲、乙二人在该商区临时停车，两人停车都不超过
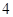小时．
（1）若甲停车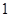小时以上且不超过
小时的概率为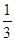
，停车付费多于
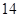元的概率为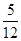
，求甲停车付费恰为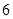元的概率；
（2）若每人停车的时长在每个时段的可能性相同，求甲、乙二人停车付费之和为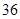
元的概率．
（本小题满分12分）设数列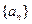
的前n项和为
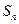，且
（Ⅰ）设
，求证：数列
是等比数列；
（Ⅱ）求数列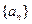的通项公式．
（本小题满分12分）
已知数列
（I）求
的通项公式；
（II）求证：
（本小题满分12分）
已知A、B是抛物线
上的两点，O是抛物线
的顶点，OA⊥OB。
（I）求证：直线AB过定点M（4，0）；
（II）设弦AB的中点为
P，求点P到直线
的距离的最小值。
（本小题满分12
分）
已知函数
（I）证明：函数
；
（II）设函数
在（—1，1）上单调递增，求a的取值范围。
（本小题满分13分）
如图，三棱锥P—ABC中，平面PAC⊥平面BAC，AP=AB=AC=2，∠BAC=∠PAC=12
0°。
（I）求棱PB的长；
（II）求二面角P—AB—C的大小。