如图,在正方形ABCD中, AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.

(1)求证:∠GCF=∠FCE;
(2)判断线段PG,PB与DG之间的数量关系,并证明你的结论;
(3)若BP=2,在直线AB上是否存在一点M,使四边形DMPF是平行四边形,若存在,求出BM的长度,若不存在,说明理由.
.
如图,在正方形ABCD内,已知两个动圆⊙O1与⊙Q2互相外切.且⊙O1与边AB,AD相切,⊙O2与边BC,CD相切,若正方形的边长为1,⊙O1与⊙Q2的半径分别为 ,
, .
.
(1)求
 和
和 的关系式;
的关系式;(2)求⊙O1与⊙Q2的面积之和的最小值.
某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为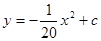 且过顶点C(0,5)(长度单位:m)
且过顶点C(0,5)(长度单位:m)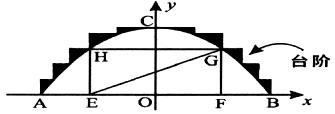
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5 m的地毯,地毯的价格为20元/m2,求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右测上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求点G的坐标.
.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC:
(2)若AB=4,AD=3
 ,AE=3,求AF的长.
,AE=3,求AF的长.
如图:是7×7的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-4,2),B点坐标为(-2,4).
(2)在第二象限内格点上找一点C,使C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是_________;△ABC周长是____________.(结果保留根号)
(3)画出三角形ABC以O为位似中心,相似比为
 的位似图形.
的位似图形.
中央电视台举办的第14届“蓝色经典·天之蓝”杯青年歌手大奖赛,由部队文工团的A(海政)、B(空政)、C(武警)组成种子队,由部队文工团的D(解放军)和地方文工团的E(云南)、F(新疆)组成非种子队.现从种子队A、B、C与非种子队D、E、F中各抽取一个队进行首场比赛.(1)请用适当方式写出首场比赛出场的两个队的所有可能情况(用代码A、B、C、D、E、F表示);
(2)求首场比赛出场的两个队都是部队文工团的概率P.