如图，已知矩形ABCD，AB=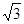
，BC=3，在BC上取两点E，F（E在F左边），以时为边作等边三角形PEF，使顶点P在AD上，PE，PF分别交AC于点G，H．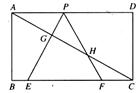
（1）求△PEF的边长；
（2）在不添加辅助线的情况下，当F与C不重合时，从图中找出一对相似三角形 （不含全等形），并证明；
（3）若△PEF的边EF在线段BC上以每秒1个单位的速度移动．设BE的长为
，PH的长为
，请你写出与的函数式，并指出函数自变量的取值范围．
三角形两边长分别是8和6，第三边的长是一元二次方程x2－16x+60=0的一个实数根，求此三角形的面积．
如图，AB为⊙O直径，BC切⊙O于B，CO交⊙O于D，AD的延长线交BC于E，若∠C = 25°，求∠A的度数．
解一元二次方程：（1）（x+1）2=3
（2）3y2+4y+1=0
化简二次根式：（1）
（2）
（
＜0）
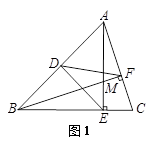
问题1已知：如图1，三角形ABC中，点D是AB边的中点，AE⊥BC，BF⊥AC，垂足分别为点E，F，AE，BF交于点M，连接DE，DF．若DE=
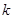DF，则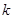的值为____
_． 
拓展
问题2已知：如图2，三角形ABC中，CB=CA，点D是AB边的中点，点M在三角形ABC的内部，且∠MAC=∠MBC，过点M分别作ME⊥BC，MF⊥AC，垂足分别为点E，F，连接DE，DF．求证：DE=DF．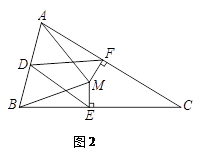
推广
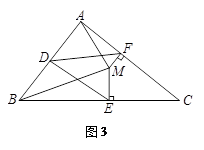
问题3如图3，若将上面问题2中的条件“CB=CA”变为“CB≠CA”，其他条件不变，试探究DE与DF之间的数量关系，并证
明你的结论．