已知函数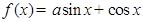 ,其中
,其中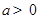 .
.
(Ⅰ)当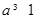 时,判断
时,判断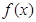 在区间
在区间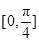 上的单调性;
上的单调性;
(Ⅱ)当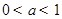 时,若不等式
时,若不等式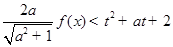 对于
对于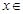
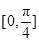 恒成立,求实数
恒成立,求实数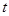 的取值范围.
的取值范围.
先后随机投掷2枚正方体骰子,其中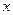 表示第
表示第 枚骰子出现的点数,
枚骰子出现的点数,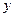 表示第
表示第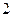 枚骰子出现的点数。设点P的坐标为
枚骰子出现的点数。设点P的坐标为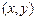 。
。
(Ⅰ)求点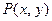 在直线
在直线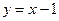 上的概率;
上的概率;
(Ⅱ)求点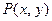 满足
满足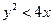 的概率。
的概率。
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(Ⅰ)用茎叶图表示这两组数据;若将频率视为概率,对甲学生在培训后参加的一次数学竞赛成绩进行预测,求甲的成绩高于80分的概率;
(Ⅱ)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由
某学科的试卷中共有12道单项选择题,(每个选择题有4个选项,其中仅有一个选项是正确的,答对得5分,不答或答错得0分)。某考生每道题都给出了答案,已确定有8道题答案是正确的,而其余的题中,有两道题每题都可判断其两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜。对于这12道选择题,试求:
(1)该考生得分为60分的概率;
(2)该考生所得分数ξ的分布列及数学期望Eξ.
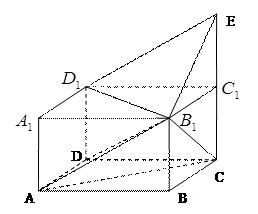
如图,在长方体 中,点
中,点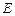 在棱
在棱 的延长线上,且
的延长线上,且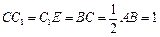 .
.
(Ⅰ)求证: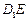 ∥平面
∥平面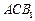 ;
;
(Ⅱ)求证:平面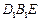
 平面
平面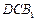 ;
;
(Ⅲ)求四面体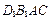 的体积.
的体积.
已知直线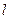 的极坐标方程为
的极坐标方程为 ,曲线C的
,曲线C的
参数方程为 ,设
,设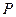 点是曲线C上的任意一点,求
点是曲线C上的任意一点,求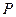 到直线
到直线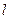 的距离的最大值.
的距离的最大值.