先后随机投掷2枚正方体骰子,其中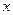 表示第
表示第 枚骰子出现的点数,
枚骰子出现的点数,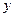 表示第
表示第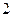 枚骰子出现的点数。设点P的坐标为
枚骰子出现的点数。设点P的坐标为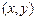 。
。
(Ⅰ)求点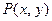 在直线
在直线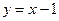 上的概率;
上的概率;
(Ⅱ)求点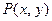 满足
满足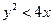 的概率。
的概率。
在等比数列 中,
中, ,公比
,公比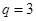 ,前
,前 项和
项和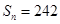 ,求首项
,求首项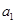 和项数
和项数 .
.
△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积.
已知直线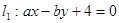 和直线
和直线 ,直线
,直线 过点
过点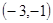 ,并且直线
,并且直线 和
和 垂直,求
垂直,求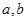 的值。
的值。
某地上年度电价为0.8元,年用电量为1亿千瓦时,本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至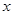 元,则本年度新增用电量
元,则本年度新增用电量 (亿千瓦时)与(
(亿千瓦时)与(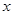 -0.4)元成反比例.又当
-0.4)元成反比例.又当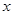 =0.65时,
=0.65时, =0.8.
=0.8.
(1)求 与
与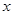 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益=用电量×(实际电价-成本价)]
已知 ,
,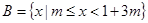 .
.
(1)当m=1时,求A∪B;
(2)若B⊆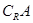 ,求实数m的取值范围.
,求实数m的取值范围.