已知函数 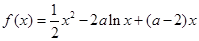 ,
,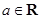 .
.
(1)当 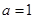 时,求函数
时,求函数 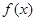 的最小值;
的最小值;
(2)当  时,讨论函数
时,讨论函数 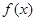 的单调性;
的单调性;
(3)是否存在实数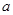 ,对任意的
,对任意的 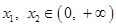 ,且
,且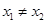 ,有
,有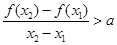 ,恒成立,若存在求出
,恒成立,若存在求出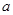 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
如图,正方形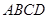 所在平面与圆
所在平面与圆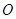 所在平面相交于
所在平面相交于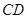 ,线段
,线段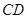 为圆
为圆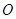 的弦,
的弦,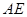 垂直于圆
垂直于圆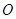 所在平面,垂足
所在平面,垂足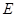 是圆
是圆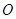 上异于
上异于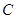 、
、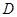 的点,
的点,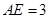 ,圆
,圆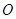 的直径为9。
的直径为9。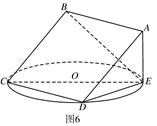
(1)求证:平面 平面
平面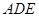 ;
;
(2)求二面角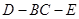 的平面角的正切值。
的平面角的正切值。
深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球).每次训练,都从中任意取出2个球,用完后放回.
(1)设第一次训练时取到的新球个数为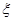 ,求
,求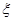 的分布列和数学期望;
的分布列和数学期望;
(2)求第二次训练时恰好取到一个新球的概率.
已知向量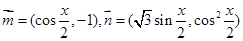 ,设函数
,设函数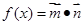 +1
+1
(1)若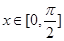 ,
, 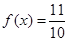 ,求
,求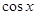 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是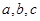 ,且满足
,且满足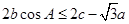 ,求
,求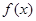 的取值范围.
的取值范围.

 已知
已知 ,
,
(1)求 解析式
解析式
(2)若函数 与
与 关于直线
关于直线 对称,若对任意实数
对称,若对任意实数
恒有 成立,求
成立,求 取值范围
取值范围