如图,正方形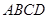 所在平面与圆
所在平面与圆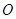 所在平面相交于
所在平面相交于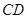 ,线段
,线段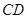 为圆
为圆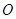 的弦,
的弦,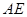 垂直于圆
垂直于圆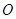 所在平面,垂足
所在平面,垂足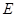 是圆
是圆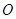 上异于
上异于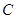 、
、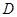 的点,
的点,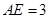 ,圆
,圆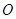 的直径为9。
的直径为9。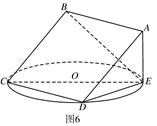
(1)求证:平面 平面
平面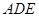 ;
;
(2)求二面角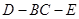 的平面角的正切值。
的平面角的正切值。
已知函数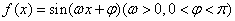 的周期为
的周期为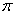 ,图像的一个对称中心为
,图像的一个对称中心为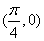 ,
,
将函数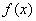 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移
图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移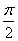 个单位
个单位
长度后得到函数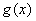 的图像.
的图像.
(1)求函数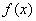 与
与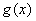 的解析式;
的解析式;
(2)是否存在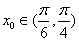 ,使得
,使得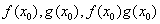 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定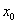 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
(3)求实数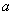 与正整数
与正整数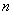 ,使得
,使得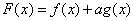 在
在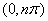 内恰有2013个零点.
内恰有2013个零点.
已知函数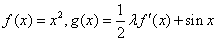 ,其中函数
,其中函数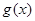 在
在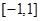 上是减函数.
上是减函数.
(1)求曲线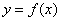 在点
在点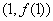 处的切线方程;
处的切线方程;
(2)若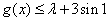 在
在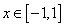 上恒成立,求
上恒成立,求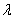 得取值范围.
得取值范围.
(3)关于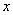 的方程
的方程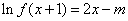 ,
,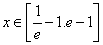 有两个实根,求
有两个实根,求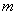 的取值范围.
的取值范围.
如图分别是正三棱台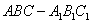 的直观图和正视图,
的直观图和正视图,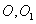 分别是上下底面的中心,
分别是上下底面的中心,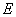 是
是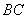 中点.
中点.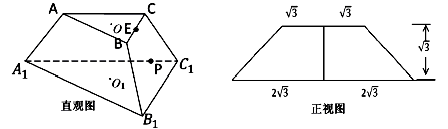
(1)求正三棱台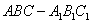 的体积;(注:棱台体积公式:
的体积;(注:棱台体积公式: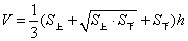 ,其中
,其中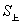 为棱台上底面面积,
为棱台上底面面积,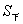 为棱台下底面面积,
为棱台下底面面积,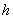 为棱台高);
为棱台高);
(2)求平面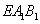 与平面
与平面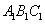 的夹角的余弦;
的夹角的余弦;
(3)若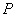 是棱
是棱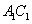 上一点,求
上一点,求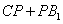 的最小值.
的最小值.
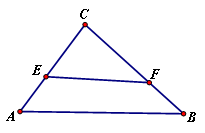
 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰 的长为3(百米),底
的长为3(百米),底 的长为4(百米).现决定在空地内筑一条笔直的小路
的长为4(百米).现决定在空地内筑一条笔直的小路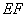 (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等,面积分别为
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等,面积分别为 和
和 .
.
(1)若小路一端 为
为 的中点,求此时小路的长度;
的中点,求此时小路的长度;
(2)若小路的端点 两点分别在两腰上,求
两点分别在两腰上,求 得最小值.
得最小值.
已知数列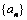 满足
满足 .
.
(Ⅰ)证明数列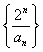 是等差数列;
是等差数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)设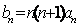 ,求数列
,求数列 的前
的前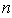 项和
项和 .
.