某地上年度电价为0.8元,年用电量为1亿千瓦时,本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至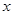 元,则本年度新增用电量
元,则本年度新增用电量 (亿千瓦时)与(
(亿千瓦时)与(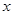 -0.4)元成反比例.又当
-0.4)元成反比例.又当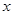 =0.65时,
=0.65时, =0.8.
=0.8.
(1)求 与
与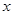 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益=用电量×(实际电价-成本价)]
设命题p: ;命题q:
;命题q:  ,若
,若 是
是 的必要不充分条件,
的必要不充分条件,
(1)p是q的什么条件?
(2)求实数a的取值范围.
某工厂某种产品的年固定成本为250万元,每生产 千件,需另投入成本为
千件,需另投入成本为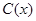 ,当年产量不足80千件时,
,当年产量不足80千件时,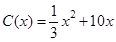 (万元)。当年产量不小于80千件时,
(万元)。当年产量不小于80千件时, (万元)。每件商品售价为0.05万元。通过市场分析,该厂生产的商品能全部售完。
(万元)。每件商品售价为0.05万元。通过市场分析,该厂生产的商品能全部售完。
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
已知各项均为正数的数列 前n项和为
前n项和为 ,首项为
,首项为 ,且
,且 成等差数列。
成等差数列。
(1)求数列 的通项公式;
的通项公式;
(2)若 ,设
,设 ,求数列
,求数列 的前n项和
的前n项和 .
.
几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.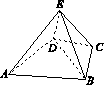
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高.然而也有部分公众对该活动的实际效果与负面影响提出了疑问.对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 |
保留 |
不支持 |
|
| 20岁以下 |
800 |
450 |
200 |
| 20岁以上(含20岁) |
100 |
150 |
300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取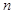 个人,已知从“支持”态度的人中抽取了45人,求
个人,已知从“支持”态度的人中抽取了45人,求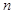 的值;
的值;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有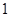 人20岁以下的概率;
人20岁以下的概率;