(本小题满分12分)已知锐角△ABC中的三个内角分别为A,B,C.
(1)设 ,求证△ABC是等腰三角形;
,求证△ABC是等腰三角形;
(2)设向量s=(2sinC,- ),t=(cos2C,2
),t=(cos2C,2 -1),且s∥t,若sinA=
-1),且s∥t,若sinA= ,求sin(
,求sin( -B)的值.
-B)的值.
(本小题满分10分)某校要进行特色学校评估验收,有甲、乙、丙、丁、戊五位评估员将随机去 三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
(1)求甲、乙同时去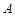 班听课的概率;
班听课的概率;
(2)设随机变量 为这五名评估员去
为这五名评估员去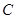 班听课的人数,求
班听课的人数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分10分)在如图所示的多面体中,四边形 为正方形,四边形
为正方形,四边形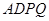 是直角梯形,
是直角梯形,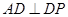 ,
, 平面
平面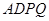 ,
,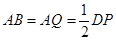 .
.
(1)求证: 平面
平面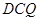 ;
;
(2)求平面 与平面
与平面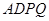 所成的锐二面角的大小.
所成的锐二面角的大小.
(不等式选讲)(本小题满分10分)已知a,b是正实数,求证: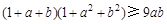 .
.
(极坐标与参数方程)(本小题满分10分) 已知曲线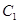 的极坐标方程为
的极坐标方程为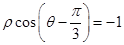 ,曲线
,曲线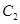 的极坐标方程为
的极坐标方程为 ,判断两曲线的位置关系.
,判断两曲线的位置关系.