如图1，已知抛物线
与一直线相交于
，
两点，与
轴交于点
，其顶点为
．
（1）求抛物线及直线
的函数关系式，并直接写出点的坐标；
（2）如图1，若抛物线的对称轴与直线相交于点
，
为直线上的任意一点，过点作
∥
交抛物线于点
，以，，，为顶点的四边形能否为平行四边形？若能，求点的坐标；若不能，请说明理由；
（3）如图2，若点
是抛物线上位于直线上方的一个动点，求
的面积的最大值．
在平面直角坐标系xOy中，过点(0，2)且平行于x轴的直线，与直线y＝x－1交于点A，点A关于直线x＝1的对称点为B，抛物线C1：y＝x2＋bx＋c经过点A，B.
(1)求点A，B的坐标；
(2)求抛物线C1的表达式及顶点坐标；
(3)若拋物线C2：y＝ax2(a≠0)与线段AB恰有一个公共点，结合函数的图象，求a的取值范围.
作平面直角坐标系xOy中，直线y＝kx＋b(k≠0)与双曲线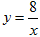
的一个交点为P(2，m)，与x轴、y轴分别交于点A，B.
(1)求m的值；
(2)若PA＝2AB，求k的值.
（本小题10分）
已知二次函数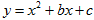
（ b，c为常数）.
（Ⅰ）当b =2，c =-3时，求二次函数的最小值；
（Ⅱ）当c =5时，若在函数值y =1的情况下，只有一个自变量x的值与其对应，求此时二次函数的解析式；
（Ⅲ）当c=b2时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式.
(本小题满分11分)
如图，已知点O(0，0)，A(－5，0)，B(2，1)，抛物线l：y＝－(x－h)2＋1(h为常数)与y轴的交点为C.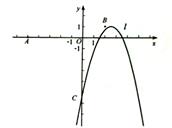
(1)l经过点B，求它的解析式，并写出此时l的对称轴及顶点坐标：
(2)设点C的级坐标为yc，求yc的最大值，此时l上有两点(x1，y1)，(x2，y2)，其中x1＞x2≥0，比较y1与y1的大小；
(3)当线段OA被l只分为两部分，且这两部分的比是1:4时，求h的值.
(本小题满分10分)
水平放置的容器内原有210毫米高的水，如图.将若干个球逐一放入容器中，每放入一个大球水面就上升4毫米，每放入一个小球水面就上升3毫米，假定放入容器中的所有球完全浸没水中且水不溢出，设水面高为y毫米.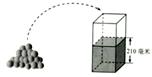
(1)只放入大球，且个数为x大，求y与x大的函数关系式(不必写出x大的范围)；
(2)仅放入6个大球后，开始放入小球，且小球个数为x小.
①求y与x小的函数关系式(不必写出x小的范围)；
②限定水面高不超过260毫米，最多放入几个小球？