近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后决定购进甲、乙两种空气净化器进行销售。.若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同。求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?
如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,求AB的长度。(可利用的围墙长度不超过3m)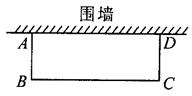
如图,Rt△ABC中∠C=90°,AD·AC=AE·AB,求证:DE⊥AB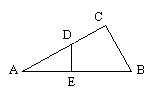
解方程 2x2-3x+1=0
在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/s的速度在线段AB上由A向B匀速运动,E点同时以1cm/s的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5)。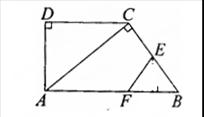
(1)求证△ACD∽△BAC;
(2)求DC的长; (3)t为何值时,四边形AFEC的面积为19。
(3)t为何值时,四边形AFEC的面积为19。
如图,已知一次函数与反比例函数的图象交于点A(-4,-2)和B(a,4)。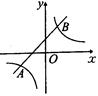
(1)求反比例函数的解析式和点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?