在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=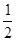 ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图1).求证:△BOG≌△POE;
(2)结合图2,通过观察、测量、猜想: =______,并证明你的猜想;
=______,并证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图3),若AC=8,BD=6,直接写出 的值.
的值.
一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY、XZ恰好分别经过点B、C.△ABC中,∠A=50°.
(1)如图1,则∠ABC+∠ACB=度,∠XBC+∠XCB=度;
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
某商场用2600元恰好购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
| 类型 价格 |
A型 |
B型 |
| 进价(元/盏) |
40 |
65 |
| 标价(元/盏) |
60 |
100 |
(1)这两种台灯各购进多少盏?
(2)由于诚信经营,原先的50盏已经销售一空,在每种台灯进价、标价不变的情况下,商场再次购进50盏台灯,问需再购进B种台灯多少盏时该商场销售这100台灯的总利润恰好是2810元?
如图是某设计师在方格纸(每个小方格均是边长为1的正方形)中设计图案的一部分,请你帮他完成余下的工作:
(1)作出关于直线AB的轴对称图形;
(2)将你画出的部分连同原图形绕点O逆时针旋转 ;
;
(3)请计算你所得到的图案的面积
任意抛掷一枚骰子两次,骰子停止转动后,计算朝上的点数的和.
(1)和最小的是多少,和最大的是多少?
(2)下列事件:①点数的和为7;②点数的和为1;③点数的和为15.哪些是不可能性事件?哪些是不确定事件?
(3)点数的和为7与点数的和为2的可能性谁大?请说明理由.
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE。试说明下列结论正确的理由:(1) ∠C=∠E; (2) AB=AD.