(本题12分)如图,把△OAB放置于平面直角坐标系xOy中,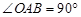 ,
,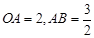 ,把△OAB沿
,把△OAB沿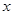 轴的负方向平移2OA的长度后得到△DCE.
轴的负方向平移2OA的长度后得到△DCE.
(1)若过原点的抛物线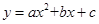 经过点B、E,求此抛物线的解析式;
经过点B、E,求此抛物线的解析式;
(2)若点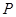 在该抛物线上移动,当点P在第一象限内时,过点
在该抛物线上移动,当点P在第一象限内时,过点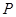 作
作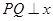 轴于点
轴于点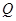 ,连结
,连结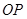 .若以
.若以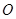 、
、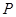 、
、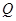 为顶点的三角形与以B、C、E为顶点的三角形相似,直接写出点
为顶点的三角形与以B、C、E为顶点的三角形相似,直接写出点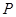 的坐标;
的坐标;
(3)若点M(-4,n) 在该抛物线上,平移抛物线,记平移后点M的对应点为M′,点B的对应点为B′.当抛物线向左或向右平移时,是否存在某个位置,使四边形M′B′CD的周长最短?若存在,求出此时抛物线的解析式;若不存在,请说明理由.