(本小题满分14分)
某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台.现销售给A地10台,B地8台.已知从甲地调运1台至A地、B地的运费分别为400元和800元,从乙地调运1台至A地、B地的费用分别为300元和500元.
(1)设从甲地调运x台至A地,求总费用y关于台数x的函数解析式;
(2)若总运费不超过9000元,问共有几种调运方案;
(3)求出总运费最低的调运方案及最低的费用.
(本小题满分15分)如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,已知AB=a,AC=2,AA1=1,点D在棱B1C1上,且B1D∶DC1=1∶3.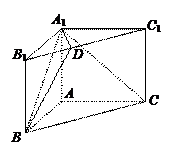
(Ⅰ)证明:BD⊥A1C;
(Ⅱ)若二面角B-A1D-B1的大小为60º,试求a的值.
(本小题满分14分)将3个完全相同的小球随机地放入编号依次为1,2,3,4,5的盒子里,用随机变量 表示有球盒子编号的最大值.(Ⅰ)求
表示有球盒子编号的最大值.(Ⅰ)求 ;(Ⅱ)求
;(Ⅱ)求 的分布列和数学期望
的分布列和数学期望
 .
.
已知过点 (
( ,0)(
,0)( )的动直线
)的动直线 交抛物线
交抛物线 于
于 、
、 两点,点
两点,点 与点
与点 关于
关于 轴对称.(I)当
轴对称.(I)当 时,求证:
时,求证: ;
; (II)对于给定的正数
(II)对于给定的正数 ,是否存在直线
,是否存在直线 :
: ,使得
,使得 被以
被以 为直径的圆所截得的弦长为定值?如果存在,求出的
为直径的圆所截得的弦长为定值?如果存在,求出的
 方程;如果不存在,试说明理由.
方程;如果不存在,试说明理由.
函数 在
在 处取得极小值–2.(I)求
处取得极小值–2.(I)求 的单调区间;(II)若对任意的
的单调区间;(II)若对任意的 ,函数
,函数 的图像
的图像 与函数
与函数 的图像
的图像 至多有一个交点.求实数
至多有一个交点.求实数 的范围.
的范围.
已知点(1,2)是函数 的图象上一点,数列
的图象上一点,数列 的前
的前 项和为
项和为 .(I)求数列
.(I)求数列 的通项公式;(II)若
的通项公式;(II)若 ,求数列
,求数列 的前
的前 项和.
项和.