某房屋开发公司用100万元购得一块土地,该地可以建造每层1000m2的楼房,楼房的总建筑面积(即各层面积之和)每平方米平均建筑费用与建筑高度有关,楼房每升高一层,整幢楼房每平方米建筑费用增加20元。已知建筑5层楼房时,每平方米建筑费用为400元,公司打算造一幢高于5层的楼房,为了使该楼房每平方米的平均综合费用最低(综合费用是建筑费用与购地费用之和),公司应把楼层建成几层?
已知在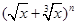 (其中n<15)的展开式中:
(其中n<15)的展开式中:
(1)求二项式展开式中各项系数之和;
(2)若展开式中第9项,第10项,第11项的二项式系数成等差数列,求n的值;
(3)在(2)的条件下写出它展开式中的有理项.
3名教师与4名学生排成一横排照相,求:
(1)3名教师必须排在一起的不同排法有多少种?
(2)3名教师必须在中间(在3、4、5位置上)的不同排法有多少种?
(3)3名教师不能相邻的不同排法有多少种?
已知复数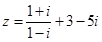 .求
.求
(1)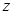 ;(2)
;(2)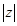 .
.
数列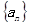 的前
的前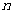 项和为
项和为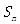 ,且
,且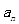 是
是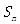 和1的等差中项,等差数列
和1的等差中项,等差数列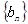 满足
满足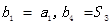 .
.
(1)求数列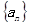 ,
,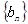 的通项公式;
的通项公式;
(2)设 ,数列
,数列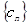 的前n项和为
的前n项和为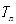 ,若
,若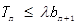 对一切
对一切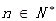 恒成立,求实数
恒成立,求实数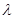 的最小值.
的最小值.
已知向量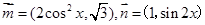 ,函数
,函数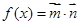 .
.
(1)求函数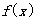 的对称中心;
的对称中心;
(2)在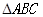 中,
中,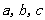 分别是角
分别是角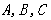 对边,且
对边,且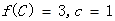 ,且
,且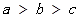 ,求
,求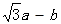 的取值范围.
的取值范围.