(12分)已知 p:
p: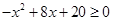 ,q:
,q: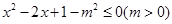 .
.
(Ⅰ)若p是q充分不必要条件,求实数 的取值范围;
的取值范围;
(Ⅱ)若“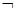 p”是“
p”是“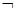 q”的充分不必要条件,求实数
q”的充分不必要条件,求实数 的取值范围.
的取值范围.
(本小题满分12分)
等比数列 中,
中,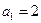 ,
,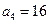 .
.
(1)求数列 的通项公式.
的通项公式.
(2)若 分别是等差数列
分别是等差数列 的第三项和第五项,试求数列
的第三项和第五项,试求数列 的通项
的通项
公式及前 项和
项和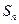 .
.
本小题满分10分)
已知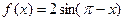 sin
sin .
.
(1)求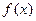 的最小正周期.
的最小正周期.
(2)若A,B,C是锐角△ABC的内角,其对边分别是 ,且
,且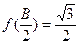 ,
,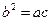
试判断△ABC的形状.
选修4—5:不等式选讲。设函数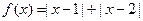
(1)求不等式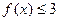 的解集;
的解集;
(2)若不等式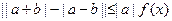 (
(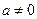 ,
,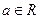 ,
,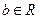 )恒成立,求实数
)恒成立,求实数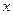 的范围.
的范围.
选修4—4:坐标系与参数方程。在极坐标系中,如果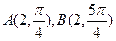 为等边三角形ABC的两个顶点,求顶点C的极坐标.(
为等边三角形ABC的两个顶点,求顶点C的极坐标.(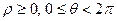 )
)
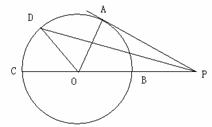
选修4—1:几何证明选讲。如图,PA切圆O于点A,割线PBC经过圆心O,
OB=PB=1,OA绕点O逆时针旋转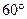 到OD.
到OD.
(1)求线段PD的长;
(2)在如图所示的图形中是否有长度为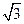 的线段?若有,指出该线段;若没有,说明理由.
的线段?若有,指出该线段;若没有,说明理由.