已知函数 .
.
(Ⅰ)若函数在区间 上有最小值
上有最小值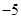 ,求
,求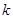 的值.
的值.
(Ⅱ)若同时满足下列条件①函数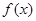 在区间
在区间 上单调;②存在区间
上单调;②存在区间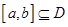 使得
使得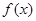 在
在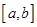 上的值域也为
上的值域也为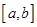 ;则称
;则称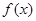 为区间
为区间 上的闭函数,试判断函数
上的闭函数,试判断函数 是否为区间
是否为区间 上的闭函数?若是求出实数
上的闭函数?若是求出实数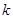 的取值范围,不是说明理由.
的取值范围,不是说明理由.
(本小题满分12分) 已知等差数列 的前n项和为
的前n项和为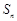 ,且
,且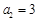 ,
,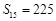 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设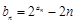 ,求数列
,求数列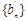 的前n项和
的前n项和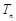 .
.
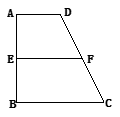
(本小题满分14分)已知梯形ABCD中,AD∥BC,∠ABC =∠BAD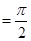 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE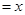 ,G是BC的中点.沿EF将梯形ABCD翻折,
,G是BC的中点.沿EF将梯形ABCD翻折,
使平面AEFD⊥平面EBCF (如图).
(1)当 时,求证:BD⊥EG ;
时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为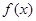 ,求
,求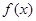 的最大值;
的最大值;
(3)当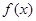 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.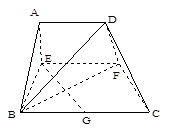
(本小题满分12分)如图所示,正方形 和矩形
和矩形 所在平面相互垂直,
所在平面相互垂直, 是
是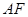 的中点.
的中点.
(1)求证: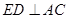 ;
;
(2)若直线 与平面
与平面 成45o角,求异面直线
成45o角,求异面直线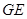 与
与 所成角的余弦值.
所成角的余弦值.
(本小题满分12分)如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠DAB=60°.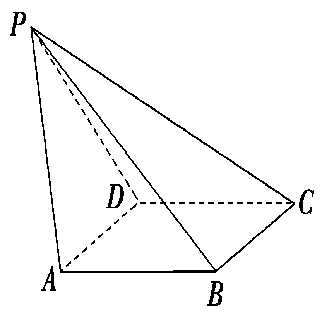
(1)证明:∠PBC=90°;
(2)若PB=3,求直线AB与平面PBC所成角的正弦值.
(本小题满分12分)如图:在三棱锥 中,已知点
中,已知点 、
、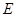 、
、 分别为棱
分别为棱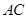 、
、 、
、 的中点.
的中点.
(1)求证: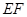 ∥平面
∥平面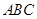 ;
;
(2)若 ,
,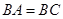 ,求证:平面
,求证:平面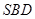 ⊥平面
⊥平面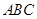 .
.