已知椭圆,过点且不过点的直线与椭圆交于
两点,直线与直线交于点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若垂直于轴,求直线的斜率;
(Ⅲ)试判断直线与直线的位置关系,并说明理由.

甲打靶射击,有4发子弹,其中有一发是空弹.
(1)求空弹出现在第一枪的概率;
(2)求空弹出现在前三枪的概率;
(3)如果把空弹换成实弹,甲前三枪在靶上留下三个两两距离分别为3,4,5的弹孔 ,第四枪瞄准了三角形
,第四枪瞄准了三角形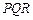 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形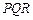 内
内 ,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
..如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米。
(1)设 (单位:米),要使花
(单位:米),要使花 坛AMPN的面积大于32平方米,求
坛AMPN的面积大于32平方米,求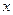 的取值范围;
的取值范围;
|
(2)若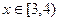 (单位:米),则当AM,A
(单位:米),则当AM,A N的长度分别是多少
N的长度分别是多少 时,花坛AMPN的面积最大?并求出最大面积。
时,花坛AMPN的面积最大?并求出最大面积。
.已知函数
 .
.
(1)求证: 在(0,+∞)上是增函数;
在(0,+∞)上是增函数;
(2)若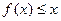 在(0,+∞)上恒成立,求
在(0,+∞)上恒成立,求 的取值范围。
的取值范围。
.已知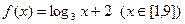 ,求函数
,求函数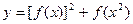 的最大值。
的最大值。