选修4-1:几何证明选讲
如图,为等腰三角形内一点,圆与的底边交于、两点与底边上的高交于点,与、分别相切于、两点.
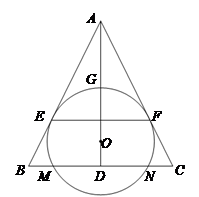
(Ⅰ)证明:;
(Ⅱ) 若等于的半径,且,求四边形的面积.
如图在四棱锥 中,底面
中,底面 是菱形,
是菱形, ,平面
,平面 平面
平面 ,
, ,
, 为
为 的中点,
的中点, 是棱
是棱 上一点,且
上一点,且 .
.
(1)求证: 平面
平面 ;
;
(2)证明: ∥平面
∥平面 ;
;
(3)求二面角 的度数.
的度数.
某校举行中学生“日常生活小常识”知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题者则被淘汰.已知选手甲答对每个题的概率均为 ,且相互间没有影响.
,且相互间没有影响.
(1)求选手甲进入复赛的概率;
(2)设选手甲在初赛中答题的个数为 ,试求
,试求 的分布列和数学期望.
的分布列和数学期望.
已知 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且满足
,且满足
(1)求角 ;
;
(2)若 ,
, ,求
,求 ,
, 的值.
的值.
我们把一系列向量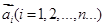 排成一列,称为向量列,记作
排成一列,称为向量列,记作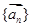 ,又设
,又设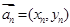 ,假设向量列
,假设向量列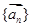 满足:
满足: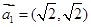 ,
,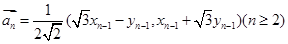 。
。
(1)证明数列 是等比数列;
是等比数列;
(2)设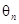 表示向量
表示向量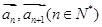 间的夹角,若
间的夹角,若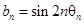 ,记
,记 的前
的前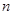 项和为
项和为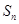 ,求
,求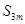 ;
;
(3)设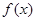 是
是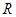 上不恒为零的函数,且对任意的
上不恒为零的函数,且对任意的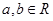 ,都有
,都有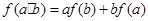 ,若
,若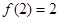 ,
, ,求数列
,求数列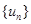 的前
的前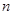 项和
项和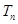 .
.
已知数列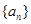 的各项均为正数,其前
的各项均为正数,其前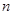 项和为
项和为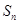 ,且
,且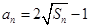 ,
,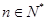 ,数列
,数列 是首项和公比均为
是首项和公比均为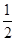 的等比数列.
的等比数列.
(1)求证数列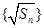 是等差数列;
是等差数列;
(2)若 ,求数列
,求数列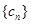 的前
的前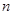 项和
项和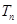 .
.