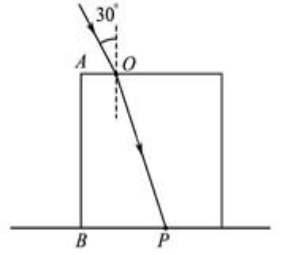
人造树脂时常用的眼镜片材料,如图所示,光线射在一人造树脂立方体上,经折射后,射在桌面上的 点,已知光线的入射角为 , , , ,求该人造树脂材料的折射率
如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC,有一质量500 g的带电小环套在直杆上,正以某一速度,沿杆匀速下滑,小环离开杆下端(C端,距地面高度h="0.8" m)后正好通过C端的正下方P点处.(g取10 m/s2)求: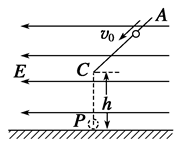
(1)小环离开直杆后运动的加速度大小和方向.
(2)小环从C运动到P点过程中动能的增量.
(3)环在直杆上匀速运动速度的大小v0.
如图所示,一质量为m的滑块从高为h的光滑圆弧形槽的顶端A处无初速度地滑下,圆弧的半径为R, 槽的底端B与水平传A带相接,传送带的运行速度为v0,长为L,滑块滑到传送带上后做匀加速运动,滑到传送带右端C时,恰好被加速到与传送带的速度相同,求: 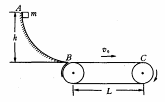
(1)滑块到达底端B时对轨道的压力F
(2)滑块与传送带间的动摩擦因数μ
(3)此过程(即滑块在传送带上运动)的时间
如图所示,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一小球
a和b。a球质量为2m,静置于地面;b球质量为3m,用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b后,求a可达到的最大高度.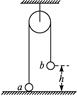
如图所示,一质量为M=4 kg,长为L=2 m的木板放在水平地面上,已知木板与地面间的动摩擦因数为0.1,在此木板的右端上还有一质量为m=1 kg的铁块,且视小铁块为质点,木板厚度不计.今对木板突然施加一个水平向右的拉力.
(1)若不计铁块与木板间的摩擦,且拉力大小为6 N,则小铁块经多长时间将离开木板?
(2)若铁块与木板间的动摩擦因数为0.2,铁块与地面间的动摩擦因数为0.1,要使小铁块对地面的总位移不超过1.5 m,则施加在木板水平向右的拉力应满足什么条件?(g=10 m/s2)
某校举行托乒乓球跑步比赛,赛道为水平直道,比赛距离为s.比赛时.某同学将球置于球拍中心,以大小为a的加速度从静止开始做匀加速直线运动,当速度达到v0时,再以v0做匀速直线运动跑至终点.整个过程中球一直保持在球拍中心不动.比赛中,该同学在匀速直线运动阶段保持球拍的倾角为θ0,如图所示,设球在运动中受到的空气阻力大小与其速度大小成正比,方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g.
(1)求空气阻力大小与球速大小的比例系数k;
(2)求在加速跑阶段球拍倾角θ随速度v变化的关系式;
(3)整个匀速跑阶段,若该同学速度仍为v0,而球拍的倾角比θ0大了β并保持不变,不计球在球拍上的移动引起的空气阻力变化,为保证到达终点前球不从球拍上距离中心为r的下边沿掉落,求β应满足的条件.