为了考察冰川融化的状况,一支科考队在某冰川上设定一个以大本营O为圆心,半径为4km 圆形考察区域,线段P1P2是冰川的部分边界线(不考虑其它边界),当冰川融化时,边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年,冰川的边界线P1P2移动的距离为s(km),并且s与n(n为正整数)的关系是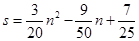 .以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(-4,9)、(-13,-3).
.以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(-4,9)、(-13,-3).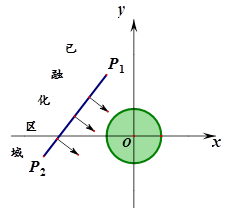
(1)求线段P1P2所在的直线对应的函数关系式;
(2)求冰川的边界线移动到考察区域所需要的最短时间.
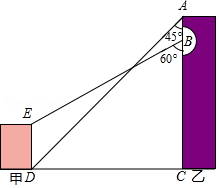
如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶 点处看甲楼楼底 点处的俯角为 ,走到乙楼 点处看甲楼楼顶 点处的俯角为 ,已知 , .求乙楼的高度 的长.(参考数据: , ,精确到 .
为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级: 级:非常满意; 级:满意; 级:基本满意; 级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
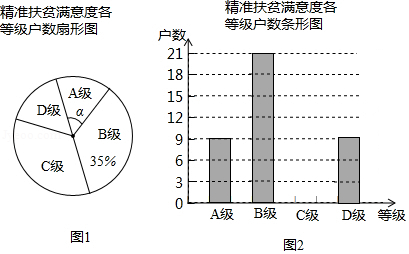
(1)本次抽样调查测试的建档立卡贫困户的总户数是 .
(2)图1中, 的度数是 ,并把图2条形统计图补充完整.
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?
(4)调查人员想从5户建档立卡贫困户(分别记为 , , , , 中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户 的概率.
如图,在四边形 中, ,点 是对角线 的中点,过点 作 的垂线,分别交 、 于点 、 ,连接 、 .试判断四边形 的形状,并证明.
先化简,再求值: ,其中 .
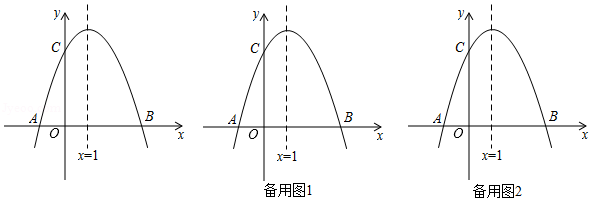
如图,已知抛物线 与 轴交于 、 两点, ,交 轴于点 ,对称轴是直线 .
(1)求抛物线的解析式及点 的坐标;
(2)连接 , 是线段 上一点, 关于直线 的对称点 正好落在 上,求点 的坐标;
(3)动点 从点 出发,以每秒2个单位长度的速度向点 运动,过 作 轴的垂线交抛物线于点 ,交线段 于点 .设运动时间为 秒.
①若 与 相似,请直接写出 的值;
② 能否为等腰三角形?若能,求出 的值;若不能,请说明理由.